Hva er sammenhengen mellom tråddelene og kaninbestanden?

I 1202 publiserte den italienske matematikeren Leonardo Fibonacci sitt verk med tittelen "The Book of the Abacus" ("Book of Calculations"), der han også beskrev serien med numre udødeliggjort med hans navn. I et av kapitlene prøver Fibonacci matematisk å vise hvordan antallet kaniner vil øke. Han vurderte følgende hypoteser som forhold:

1) de to første månedene gir et par kaniner ikke avkom;

2) fra den tredje måneden gir et par kaniner et annet par kaniner.

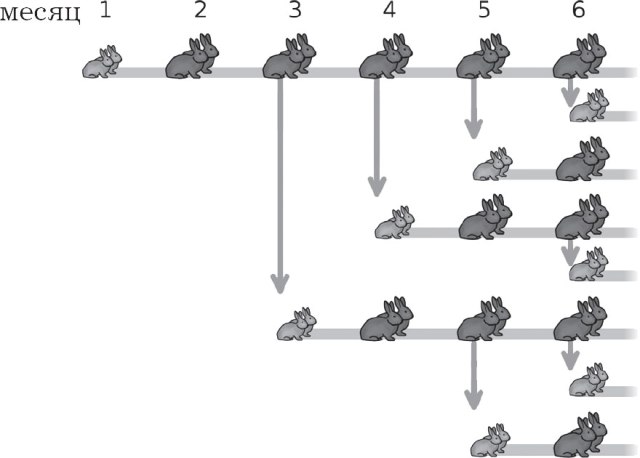
Som et resultat av å konstruere et vekstmønster for kaninbestanden, oppnår vi følgende antall serier, og legger merke til økningen i antall kaniner hver måned:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

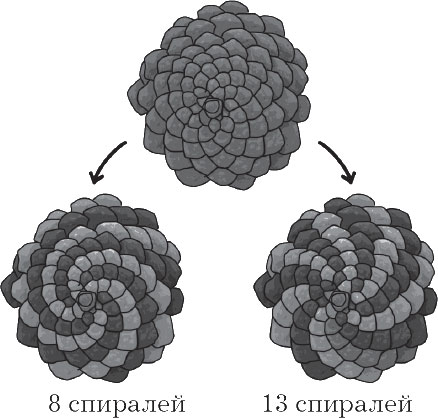
Hvis du nøye ser på støtet, vil du se at overflaten består av skalaer som er vridd i en spiral i samsvar med Fibonacci-sekvensen. Mens de er i en ananas eller i en solsikkeblomst, er de synlige for det blotte øye.

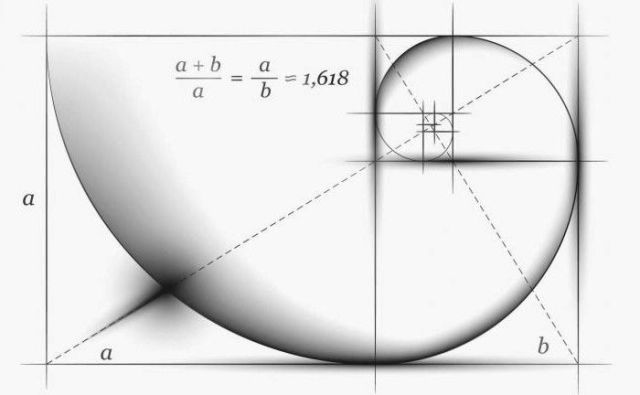
Siden tiden fra antikken til den gyldne forhold, er tallet = 1,618. De gamle grekerne vurderte verdien av ideell andel. Det gylne forholdet er forholdet mellom hvert påfølgende tall i Fibonacci-serien og det forrige:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

De gamle grekere brukte det i arkitektur. Fasaden til Parthenon i Athen har veldig like proporsjoner med et rektangel bygget på prinsippet om det gyldne forhold.

Så hva er det fine med sekvensen av ledningsseksjoner, nominelle strømmer av elektriske og avstengningsstrømmer til effektbrytere? Bygg en rekke tall med følgende verdier: 1,5; 2,5; 4; 6; 10; 16; 25; 40; 63...

Nominelle strømmer av elektromagnetiske forretter:

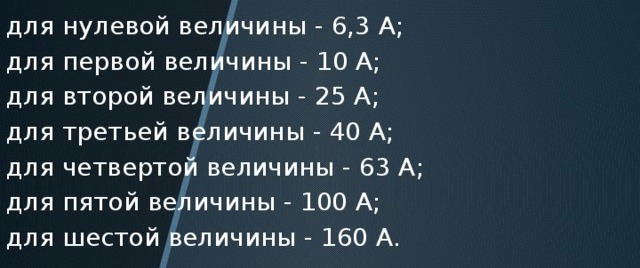
Så hvis du deler 2,5 / 1,5; 4 / 2,5; 6,3 / 4; 10 / 6,3; 16/10; 25/16; 40/25; 63/40så får vi cirka 1,6. Noe som tilsvarer gullforholdsregelen. Og gjenspeiler naturens skjønnhet og geni, selv i våre kjedelige ingeniørsystemer.

Hva tror du? Er dette en ulykke?

Basert på boken "En flott roman om matematikk. Verdenshistorie gjennom matematikkens prisme" av Michael Lone. Takk for anbefalingen fra Vladimir Kisel.

Alexey Bushnyaga