"Alt flyter," eller Ohms lov for de nysgjerrige

Til og med den siste loaferen, som har studert en stund i 10. klasse, vil fortelle læreren det Ohms lov - dette er “U er lik jeg ganger R”. Dessverre vil den smarteste utmerkede studenten si litt mer - den fysiske siden av Ohms lov vil forbli et mysterium for ham i syv seler. Jeg tillater meg å dele med kollegaene mine erfaringer med å presentere dette tilsynelatende primitive emnet.

Formålet med min pedagogiske virksomhet var kunsten og den humanitære 10. klasse, hvis viktigste interesser, som leseren antar, lå veldig langt fra fysikk. Derfor ble undervisningen i dette emnet overlatt til forfatteren av disse linjene, som generelt sett underviser i biologi. Det var for noen år siden.

Leksjonen om Ohms lov begynner med den bagatellmessige uttalelsen om at elektrisk strøm er bevegelsen av ladede partikler i et elektrisk felt. Hvis bare en elektrisk kraft virker på en ladet partikkel, vil partikkelen akselerere i samsvar med Newtons andre lov. Og hvis vektoren av elektrisk kraft som virker på den ladede partikkelen er konstant på hele banen, så er den like akselerert. Akkurat som en vekt faller under påvirkning av tyngdekraften.

Men her faller fallskjermjeger helt feil. Hvis vi forsømmer vinden, er dens fallhastighet konstant. Til og med en student i kunst- og humanitærklassen vil svare at i tillegg til tyngdekraften, virker en styrke til på den fallende fallskjermen - luftmotstandens styrke. Denne kraften er i absolutt verdi lik kraften som tiltrekker fallskjermen ved jorden og er motsatt av den i retning. Hvorfor? Dette er leksjonens viktigste spørsmål. Etter litt diskusjon konkluderer vi at dragkraften øker med økende fallrate. Derfor akselererer det fallende legemet til en hastighet hvor tyngdekraften og luftmotstanden utjevnes, og kroppen faller videre med en konstant hastighet.

Det er sant at i tilfelle av fallskjermjeger er situasjonen noe mer komplisert. Fallskjermen åpnes ikke umiddelbart, og fallskjermjegeren akselererer til betydelig høyere hastighet. Og når fallskjermen allerede har åpnet, begynner fallet med en retardasjon, som fortsetter til tyngdekraften og luftmotstandskraften er balansert.

For en fallskjermlast med en total masse m synkende med konstant hastighet v, kan vi skrive: mg - F (v) = 0, hvor F (v) Er luftmotstandskraften, ansett som en funksjon av fallhastigheten. Angående formen til funksjonen F (v) vi kan si bare en ting så langt: den vokser monotont. Det er denne omstendigheten som gir stabilisering av hastigheten.

I det enkleste tilfellet når F (v) = k, den konstante hastigheten som fallskjermen faller med vil være lik mg / k. La oss gjøre litt konvertering nå. La fallskjermen falle fra en høyde h. Da vil forskjellen i kroppens potensielle energier før og etter fallet være lik mgh = mU, hvor U er den potensielle energien til kroppen for enhetsmasse i en høyde h, eller potensialforskjellen på tyngdefeltet ved de innledende og siste innfallspunktene.

I lys av det foregående oppnår vi formelen: F (v) = mU / h. (1)

Og nå tilbake til lederen som elektrisk strøm strømmer gjennom. Et stort antall ladede partikler beveger seg langs lederen, som oftere kolliderer med atomer jo raskere de flyr. Analogien med nedstigningen av en fallskjerm er ganske gjennomsiktig, den eneste forskjellen er at det er mange "fallskjerm" og de beveger seg ikke i tyngdekraften, men i det elektriske feltet. Under disse omstendighetene kan (1) skrives om i formen: F (v) = eU / l, (2)

der e er partikkelladningen, er U den elektriske potensialforskjellen i endene av lederen, l er lengden på lederen.Strømstyrken er åpenbart lik I = neS, der n er antall ladede partikler per volumenhet, S er tverrsnittsarealet til lederen, er partikkelhastigheten (for enkelhets skyld antar vi at alle ladede partikler er like).

For å oppnå avhengigheten I (U), må du vite eksplisitt avhengigheten F (). Det enkleste alternativet (F = k) gir umiddelbart Ohms lov (I ~ U):

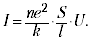
Verdien kalles ledningsevne, og gjensidigheten av den kalles motstand. Til ære for lovens oppdager er motstand vanligvis uttrykt i ohm.

Verdien (ne2 / k) kalles den spesifikke konduktiviteten, og dens inverse verdi kalles den spesifikke motstanden. Disse verdiene kjennetegner materialet som lederen består av. Det er betydelig at konduktiviteten er proporsjonal med antall ladede partikler per volumenhet (n). I metaller og elektrolyttløsninger er dette antallet stort, men i dielektrika er det lite. Antall ladede partikler per volumenhet av en gass kan avhenge av det påførte feltet (dvs. det er en funksjon av U); derfor gjelder Ohm-loven ikke for gasser.

Da vi avledet Ohms lov, gjorde vi en ikke-åpenbar antagelse. Vi godtok at kraften som hemmer bevegelsen av en ladet partikkel er proporsjonal med dens hastighet. Selvfølgelig kan man prøve å rettferdiggjøre denne ideen på en eller annen måte, men den eksperimentelle bekreftelsen ser mye mer overbevisende ut.

En eksperimentell bekreftelse av denne antagelsen er åpenbart en bekreftelse av Ohms lov i seg selv, d.v.s. proporsjonaliteten til U og I. Det ser ut til at dette ikke er vanskelig å gjøre: vi har et voltmeter og et ammeter! Akk, alt er ikke så enkelt. Vi må forklare elevene våre at et voltmeter, akkurat som et ammeter, ikke måler spenning, men strømstyrke. Og vi har rett til å stille volt på voltmeter skalaen bare fordi vi i utgangspunktet kjenner Ohms lov, som vi ønsker å sjekke. Trenger andre tilnærminger.

Du kan for eksempel bruke den følgende ideen. Vi kobler n-batterier i serie og antar at spenningen i dette tilfellet økte n ganger. Hvis Ohms lov er sann, vil den nåværende styrken også øke n ganger, på grunn av hvilken forholdet n / I (n) ikke vil avhenge av n. Denne antagelsen begrunnes av erfaring. Riktig nok har batteriene også indre motstand, og det er grunnen til at verdien til n / I (n) vokser sakte med økende n, men det er ikke vanskelig å korrigere for dette. (G. Ohm selv målte stress på en annen måte, som elevene kan lese om i læreboka til G.Ya. Myakishev og andre.)

Vi stiller spørsmålet: “I den fjerne stjernebildet Tau Ceti,” ikke Ohms lov, men loven til den store lokale forskeren Academic X. I henhold til Xs lov er strømstyrken proporsjonal med kvadratet av potensialforskjellen i endene av lederen. Hvordan avhenger av bremsekraften til partikler av deres hastighet på Tau Ceti? ” Ved hjelp av enkle transformasjoner kommer studenter til den konklusjon at styrken er proporsjonal med kvadratroten til hastighet.

Og la oss nå gå videre til en annen prosess: bevegelse av vann i et rør, i endene som forskjellige trykk opprettes. Her har vi en helt annen situasjon: ikke separate bevegelige partikler gnir mot et stasjonært materiale fordelt over hele volumet av lederen, men lag med bevegelige partikler gnir mot hverandre. Og denne omstendigheten endrer grunnleggende all fysisk resonnement.

To krefter virker på et eget lag vann som beveger seg i et rør:

a) forskjellen i trykkrefter i endene av laget;

b) friksjonskraften mot nærliggende vannlag.

Hvis det oppnås en konstant hastighet på laget, er disse kreftene like og rettet i motsatte retninger.

Friksjonsstyrken mot nærliggende vannlag kan bremse bevegelsen hvis og bare hvis forskjellige lag med vann beveger seg i forskjellige hastigheter. I en leder er ikke hastigheten på ladede partikler avhengig av om de er i kanten av lederen eller i midten, men vannet i midten av røret beveger seg raskt, og sakte langs kantene, på selve overflaten av røret, er vannhastigheten null.

En analog av strømstyrken kan betraktes som vannføring, d.v.s. mengden vann som strømmer ut av røret per tidsenhet. Siden hastigheten på vannet i forskjellige lag ikke er den samme, er det ikke så enkelt å beregne strømningshastigheten.En analog av forskjellen i elektriske potensialer er trykkforskjellen i endene av røret.

Akkurat som i en leder med strøm, observeres en direkte proporsjonalitet i røret med vann mellom trykkforskjellen i endene og strømningshastigheten. Men proporsjonalitetskoeffisienten er helt annerledes. For det første avhenger vannstrømningshastigheten ikke bare av rørets tverrsnittsareal, men også av dens form. Hvis røret er sylindrisk, er strømningshastigheten direkte proporsjonal ikke med tverrsnittsarealet, men til dets kvadrat (dvs. radius til fjerde grad). Denne avhengigheten kalles Poiseuille-loven.

Her er tiden inne for å minne om løpet av anatomi, fysiologi og hygiene, studert i 9. klasse. Menneskekroppen har et stort antall fartøyer koblet parallelt. Anta at et av disse fartøyene har utvidet seg, og radiusen har økt litt, bare to ganger. Hvor mange ganger, med samme trykk i endene av karet, vil mengden blod som passerer gjennom det øke? Tverrsnittsarealet er proporsjonalt med kvadratet med radius, og kvadratet av tverrsnittsarealet er proporsjonalt med fjerde graders radius. Derfor, når radius er doblet, øker blodstrømmen 16 (!) Ganger. Slik er kraften i Poiseuille-loven, som lar oss lage en veldig effektiv mekanisme for omfordeling av blod mellom organer. Hvis elektroner ikke strømmet gjennom blodkar, ville strømmen deres øke bare fire ganger.

Beskrivelsen ovenfor av emnet er forskjellig fra det tradisjonelle. For det første blir det brukt tre leksjoner på emnet, som med den nåværende timemangel kan betraktes som en utilregnelig luksus for naturvitenskapene. Dette begrunnes imidlertid med at det er mulig å ganske enkelt og populært avsløre lovens fysiske betydning og utstyre studentene med en metodikk som de kan bruke for å analysere en rekke fysiske prosesser: fall av en kropp i luft, bevegelse av en væske i et rør, bevegelse av ladde partikler langs en leder og senere i analysen av passering av elektrisk strøm gjennom vakuum og gjennom gasser.

Denne tilnærmingen kalles tverrfaglig integrering. Med dets hjelp demonstrerte vi for studentene fellestrekk i fjerne, første øyekast, deler av fysikk, vi viste at fysikk ikke er en "gjeng" med "fysiske lover" som ikke er forbundet med hverandre, men en smal bygning. Det samme er selvfølgelig for andre vitenskapelige fagområder. Og det virker som om et irrasjonelt sløsing med treningstimer lønner seg fullt.

Les også:Hvordan bruke en multimeter