Hva er en PID-kontroller?

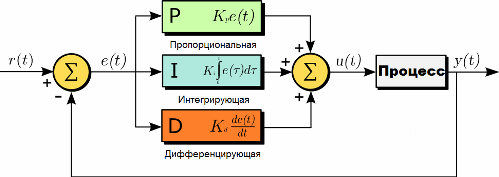
PID (fra det engelske P-proporsjonal, I-integrert, D-derivat) - en regulator er en enhet som brukes i kontrollsløyfer utstyrt med en tilbakemeldingskobling. Disse kontrollerne brukes til å generere et styresignal i automatiske systemer der det er nødvendig å oppnå høye krav til kvalitet og nøyaktighet på transienter.

Styresignalet til PID-kontrolleren oppnås ved å legge til tre komponenter: den første er proporsjonal med verdien av feilsignalet, den andre er integralen av feilsignalet, og den tredje er dens derivat. Hvis noen av disse tre komponentene ikke er inkludert i tilleggsprosessen, vil ikke kontrolleren lenger være PID, men bare proporsjonal, proporsjonal differensierende eller proporsjonalt integrerende.

Den første komponenten er proporsjonal

Utgangssignalet gir en proporsjonal komponent. Dette signalet fører til motvirkning til strømavviket for inngangsmengden som skal reguleres fra den innstilte verdien. Jo større avvik, jo større signal. Når inngangsverdien til den kontrollerte variabelen er lik den spesifiserte verdien, blir utsignalet lik null.

Hvis vi bare legger igjen denne proporsjonale komponenten og bare bruker den, vil verdien av mengden som skal reguleres aldri stabilisere seg til riktig verdi. Det er alltid en statisk feil som tilsvarer en slik verdi av avviket til den kontrollerte variabelen at utsignalet stabiliserer seg ved denne verdien.

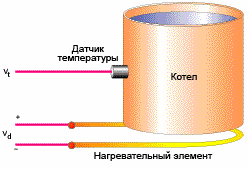
En termostat styrer for eksempel kraften til en varmeenhet. Utgangssignalet synker når den ønskede objekttemperaturen nærmer seg, og styresignalet stabiliserer kraften på varmetapet. Som et resultat vil den innstilte verdien ikke nå den innstilte verdien, fordi varmeenheten bare må slås av og begynner å kjøle seg ned (strømmen er null).

Gevinsten mellom inngang og utdata er større - den statiske feilen er mindre, men hvis forsterkningen (faktisk proporsjonalitetskoeffisienten) er for stor, så utsatt for forsinkelser i systemet (og de er ofte uunngåelige), vil selvsvingninger snart begynne i det, og hvis du øker koeffisienten er enda større - systemet vil ganske enkelt miste stabiliteten.

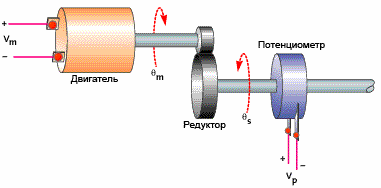
Eller et eksempel på å plassere en motor med girkasse. Med en liten koeffisient oppnås den ønskede stillingen til arbeidslegemet for sakte. Øk koeffisienten - reaksjonen vil være raskere. Men øker du koeffisienten ytterligere, vil motoren "fly over" til riktig posisjon, og systemet vil ikke raskt bevege seg til ønsket stilling, som man forventer. Hvis vi nå øker proporsjonalitetskoeffisienten ytterligere, vil svingningene begynne i nærheten av ønsket punkt - resultatet oppnås ikke igjen ...

Den andre komponenten er integrering

Tidsintegralet til misforholdet er hoveddelen av integreringsdelen. Det er proporsjonalt med dette integralet. Integreringskomponenten brukes bare for å eliminere den statiske feilen, siden kontrolleren over tid tar hensyn til den statiske feilen.

I mangel av ytre forstyrrelser vil verdien som skal reguleres etter en tid stabiliseres til riktig verdi når proporsjonalkomponenten viser seg å være null, og nøyaktigheten til utgangen vil være helt sikret av integreringskomponenten. Men integreringskomponenten kan også generere svingninger i nærheten av posisjoneringspunktet, hvis koeffisienten ikke er valgt riktig.

Den tredje komponenten er differensiering

Endringshastigheten for avviket for mengden som skal reguleres er proporsjonal med den tredje, den differensierende komponenten.Det er nødvendig for å motvirke avvik (forårsaket av ytre påvirkninger eller forsinkelser) fra riktig posisjon, spådd i fremtiden.

PID Controller Theory

Som du allerede har forstått, brukes PID-kontrollere for å opprettholde en gitt verdi x0 av en mengde, på grunn av en endring i verdien til u for en annen mengde. Det er et setpoint eller en gitt verdi x0, og det er en forskjell eller avvik (mismatch) e = x0-x. Hvis systemet er lineært og stasjonært (praktisk talt er dette knapt mulig), er følgende formler for definisjonen av u gyldige:

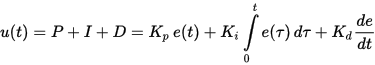
I denne formelen ser du proporsjonalitetskoeffisientene for hvert av de tre begrepene.

I praksis bruker PID-kontrollere en annen formel for innstilling, der forsterkningen brukes umiddelbart på alle komponenter:

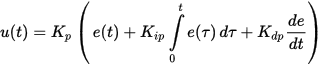
Den praktiske siden av PID-kontroll

Praktisk teoretisk analyse av PID-kontrollerte systemer brukes sjelden. Vanskeligheten er at egenskapene til kontrollobjektet er ukjente, og systemet er nesten alltid ustabilt og ikke-lineært.

Virkelig fungerende PID-kontrollere har alltid en begrensning av driftsområdet nedenfor og over, noe som forklarer deres ikke-linearitet. Derfor utføres tuning nesten alltid og overalt eksperimentelt når kontrollobjektet er koblet til kontrollsystemet.

Å bruke verdien generert av programvarekontrollalgoritmen har en rekke spesifikke nyanser. Hvis vi for eksempel snakker om temperaturkontroll, er det ofte nødvendig å ikke bare en, men to enheter på en gang: den første kontrollerer oppvarming, den andre kontrollerer kjøling. Den første leverer det oppvarmede kjølevæsken, det andre - kjølemediet. Tre alternativer for praktiske løsninger kan vurderes.

Den første ligger nær den teoretiske beskrivelsen når utgangen er en analog og kontinuerlig mengde. Den andre er en utgang i form av et pulssett, for eksempel for styring av en trinnmotor. Tredje - PWM-kontrollnår utgangen fra regulatoren tjener til å stille inn pulsbredde.

I dag er nesten alle automatiseringssystemer under bygging basert på PLS, og PID-kontrollere er spesielle moduler som blir lagt til kontrollkontrollen eller generelt implementert programmatisk ved å laste inn biblioteker. For å innstille gevinsten på slike kontrollere riktig, gir utviklerne deres spesiell programvare.