kategorier: Utvalgte artikler » Praktisk elektronikk
Antall visninger: 124786
Kommentarer til artikkelen: 1
Å ta et oscilloskopmåling
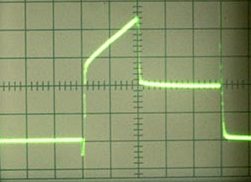Et digitalt oscilloskop er selvfølgelig mye mer perfekt enn et konvensjonelt elektronisk, det lar deg huske bølgeformer, kan koble til en datamaskin, har matematisk prosessering av resultater, skjermmarkører og mye mer. Men med alle fordelene har disse nye generasjonsenhetene en betydelig ulempe - dette er en høy pris.
Det er hun som gjør det digitale oscilloskopet utilgjengelig for amatørformål, selv om det er “lomme” oscilloskop som er verdt bare noen få tusen rubler, som selges på Aliexpress, men det er ikke spesielt praktisk å bruke dem. Vel, bare et interessant leketøy. Derfor, mens vi vil snakke om målinger ved hjelp av et elektronisk oscilloskop.
I emnet å velge et oscilloskop for bruk i et hjemmelaboratorium på Internett, kan du finne et tilstrekkelig antall fora. Uten å nekte fordelene ved digitale oscilloskop anbefales det i mange fora å velge enkle, små og pålitelige innenlandske oscilloskop C1-73 og C1-101 og lignende, som vi tidligere møtte i denne artikkelen.
Til en rimelig pris vil disse enhetene tillate deg å utføre mest amatørradiooppgaver. La oss i mellomtiden bli kjent med de generelle prinsippene for målinger ved hjelp av et oscilloskop.
Figur 1. Oscilloskop S1-73
Hva et oscilloskop måler
Det målte signalet mates til inngangen til den vertikale avbøyningskanalen Y, som har en stor inngangsmotstand, vanligvis 1MΩ, og en liten inngangskapasitans, ikke mer enn 40pF, som gjør det mulig å innføre minimal forvrengning i det målte signalet. Disse parametrene er ofte indikert ved siden av inngangen til den vertikale avbøyningskanalen.
Figur 2. Oscilloskop C1-101
Høy inngangsimpedans er typisk for voltmetre, så det er trygt å si at oscilloskopet måler spenning. Bruken av eksterne inngangsdelere lar deg redusere inngangskapasitansen og øke inngangsimpedansen. Det reduserer også påvirkningen av oscilloskopet på signalet som undersøkes.
Det må huskes at det er spesielle høyfrekvente oscilloskop, hvis inngangsimpedans bare er 50 ohm. I amatørradiopraksis finner slike enheter ikke anvendelse. Derfor vil vi videre fokusere på konvensjonelle universelle oscilloskop.
Båndbredde for Channel Y
Oscilloskopet måler spenninger i et veldig bredt område: fra likespenninger til spenninger med tilstrekkelig høy frekvens. Spenningssvingningen kan være ganske mangfoldig, fra titalls millivolt til titalls volt, og når du bruker eksterne skillelinjer opp til flere hundre volt.
Det må huskes at båndbredden til kanalen til det vertikale avviket Y DB ikke mindre enn 5 ganger høyere enn frekvensen for signalet som skal måles. Det vil si at forsterkeren av det vertikale avviket må passere minst den femte harmoniske av signalet som studeres. Dette er spesielt påkrevd når du studerer rektangulære pulser som inneholder mange harmonikker, som vist i figur 3. Bare i dette tilfellet oppnås et bilde med minimal forvrengning på skjermen.
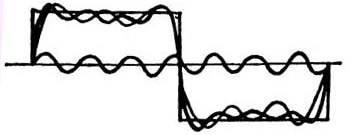
Figur 3. Syntese av et rektangulært signal fra harmoniske komponenter
I tillegg til den grunnleggende frekvensen, viser figur 3 den tredje og syvende harmonikken. Når det harmoniske tallet øker, øker frekvensen: frekvensen til den tredje harmonikken er tre ganger høyere enn den grunnleggende, den femte harmonikken er fem ganger, den syvende er syv, etc. Følgelig avtar amplituden til de høyere harmonikkene: jo høyere det harmoniske tallet, jo lavere er amplituden. Bare hvis forsterkeren til den vertikale kanalen uten mye demping kan gå glipp av de høyere harmonikkene, vil bildet av pulsen være rektangulært.
Figur 4 viser bølgeformen til en meander med utilstrekkelig båndbredde for kanal Y.
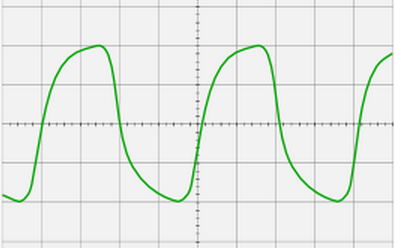
Figur 4
Slyngen med en frekvens på 500 KHz ser noe slik ut på skjermen til et OMSh-3M oscilloskop med en båndbredde på 0 ... 25 KHz. Som om rektangulære pulser ble ført gjennom en integrerende RC-krets. Et slikt oscilloskop ble produsert av sovjetisk industri for laboratoriearbeid i fysikkundervisning på skoler. Selv strømforsyningen til denne enheten av sikkerhetsmessige årsaker var ikke 220, men bare 42V. Det er helt åpenbart at et oscilloskop med en slik båndbredde vil gjøre det mulig å observere et signal med frekvenser på ikke mer enn 5 kHz uten nesten ingen forvrengning.
For et konvensjonelt universalt oscilloskop er båndbredden oftest 5 MHz. Selv med et slikt bånd kan du se et signal opp til 10 MHz og høyere, men bildet som mottas på skjermen lar deg bare bedømme tilstedeværelsen eller fraværet av dette signalet. Det vil være vanskelig å si noe om formen, men i noen situasjoner er ikke formen så viktig: for eksempel er det en bihulegenerator, og det er nok til å forsikre deg om at der er denne bihule eller ikke. Akkurat en slik situasjon er vist i figur 4.
Moderne datasystemer og kommunikasjonslinjer opererer med svært høye frekvenser, i størrelsesorden hundrevis av megahertz. For å se slike høyfrekvente signaler, må båndbredden til oscilloskopet være minst 500 MHz. Et så bredt band "utvider" virkelig prisen på oscilloskopet.
Et eksempel er det digitale oscilloskopet U1610A, ikke vist i figur 5. Båndbredden er 100 MHz, og prisen er nesten 200 000 rubler. Enig, ikke alle har råd til å kjøpe et så dyrt utstyr.
Figur 5
La ikke leseren ikke betrakte dette bildet som en annonse, siden alle koordinatene til selgeren ikke er malt over: et lignende skjermbilde kan vises på stedet for dette bildet.
Typer studerte signaler og deres parametere
Den vanligste typen svingninger i natur og teknologi er en sinusoid. Dette er den samme langmodige funksjonen Y = sinX, som ble holdt på skolen i undervisningen i trigonometri. Ganske mange elektriske og mekaniske prosesser har en sinusform, selv om det ofte brukes andre former for signaler innen elektronisk teknologi. Noen av dem er vist på figur 6.
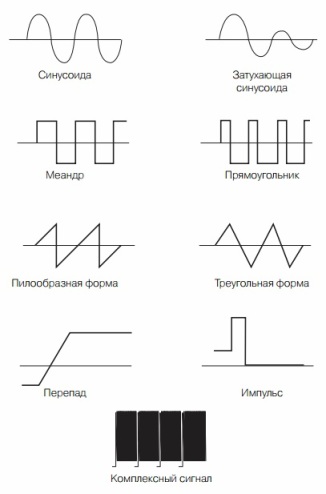
Figur 6. Former av elektriske vibrasjoner
Periodiske signaler. Signalkarakteristika
Et universelt elektronisk oscilloskop lar deg studere periodiske signaler nøyaktig. Hvis du på inngang Y sender et ekte lydsignal, for eksempel et musikalsk fonogram, vil tilfeldig flimrende burst være synlig på skjermen. Naturligvis er det umulig å undersøke et slikt signal i detalj. I dette tilfellet vil bruk av et digitalt lagringsoscilloskop hjelpe, som lar deg lagre bølgeformen.
Svingningene vist på figur 6 er periodiske, gjentatt etter en viss tidsperiode T. Dette kan vurderes mer detaljert i figur 7.
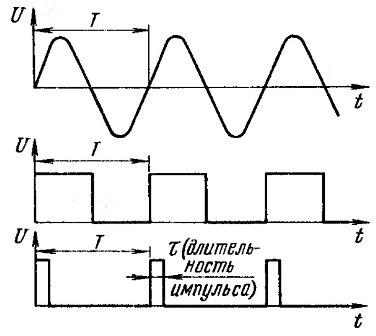
Figur 7. Periodiske svingninger
Svingningene er avbildet i et todimensjonalt koordinatsystem: spenning måles langs ordinataksen, og tiden måles langs abscisseaksen. Spenning måles i volt, tid i sekunder. For elektriske vibrasjoner blir tiden ofte målt i millisekunder eller mikrosekunder.
I tillegg til komponentene X og Y, inneholder bølgeformen også komponent Z - intensitet, eller ganske enkelt lysstyrke (figur 8). Det er hun som slår på bjelken for tidspunktet for fremre slag av bjelken og slukker for tidspunktet for returslaget. Noen oscilloskop har en inngang for å kontrollere lysstyrken, som kalles inngang Z. Hvis du bruker en pulsspenning fra en referansegenerator til denne inngangen, kan du se frekvensetikettene på skjermen. Dette lar deg mer nøyaktig måle signalets varighet langs X-aksen.
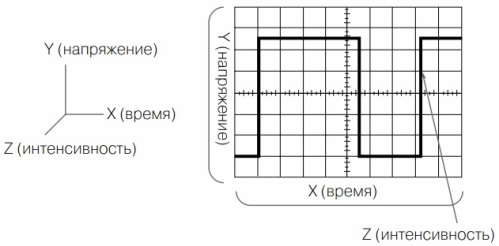
Figur 8. Tre komponenter av det undersøkte signalet
Moderne oscilloskop har som regel tidskalibrerte feier som tillater nøyaktig timing. Derfor er det praktisk talt ikke nødvendig å bruke en ekstern generator for å lage koder.
Øverst i figur 7 er en sinusbølge. Det er lett å se at det begynner i begynnelsen av koordinatsystemet. I løpet av tid T (periode) utføres en fullstendig svingning. Så gjentas alt, neste periode. Slike signaler kalles periodiske.
Rektangulære signaler er vist under sinusbølgen: bukker og rektangulær puls. De er også periodiske med periode T. Pulslengden betegnes τ (tau). Når det gjelder en slingring, er pulslengden τ lik varigheten av pausen mellom pulsene, bare halve perioden T. Derfor er bukset et spesielt tilfelle av et rektangulært signal.
Toll- og avgiftssats
For å karakterisere rektangulære pulser, brukes en parameter kalt plussyklus. Dette er forholdet mellom pulsrepetisjonstiden T og pulsvarigheten τ. For meander er driftssyklusen to, - den dimensjonsløse: S = T / τ.
I engelsk terminologi er akkurat det motsatte sant. Der kjennetegnes pulsene av driftssyklusen, forholdet mellom pulsvarighet og perioden for Duty-syklusen: D = τ / T. Fyllingsfaktoren er uttrykt i %%. Dermed 50% for meander. Det viser seg at D = 1 / S, driftssyklus og driftssyklus er gjensidig invers, selv om de kjennetegner den samme pulsparameteren. Svingens bølgeform er vist i figur 9.
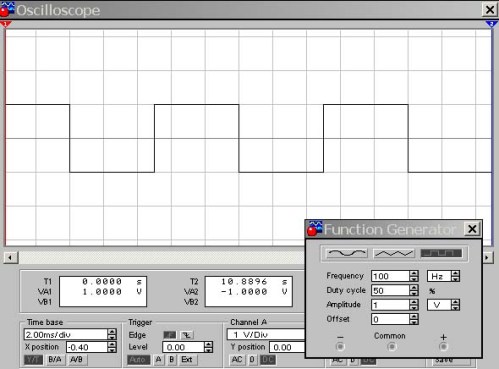
Figur 9. Bølgeform av buket D = 50%
Her er inngangen til oscilloskopet koblet til utgangen fra funksjonsgeneratoren, vist her i nedre hjørne av figuren. Og her kan en oppmerksom leser stille et spørsmål: “Amplituden til utsignalet fra 1V-generatoren, følsomheten til oscilloskopinngangen er 1V / div., Og skjermen viser rektangulære pulser med en styrke på 2V. Hvorfor? "
Fakta er at den funksjonelle generatoren genererer bipolare rektangulære pulser med hensyn til 0V-nivået, omtrent det samme som sinusbølgen, med positive og negative amplituder. Derfor blir pulser med et spenn på ± 1V observert på oscilloskopskjermen. I figuren nedenfor endrer vi for eksempel driftssyklusen til 10%.
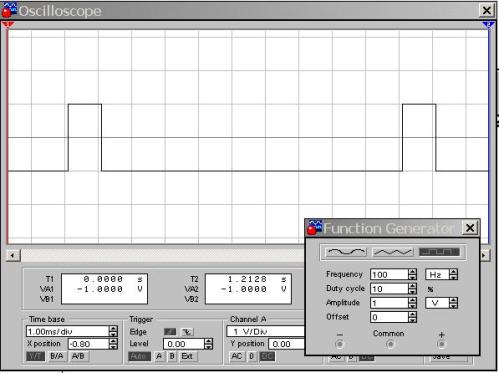
Figur 10. Rektangulært momentum D = 10%
Det er lett å se at repetisjonsperioden for puls er 10 celler, mens pulsvarigheten bare er en celle. Derfor er D = 1/10 = 0,1 eller 10%, som det fremgår av innstillingene til generatoren. Bruker du formelen for å beregne driftssyklusen, får du S = T / τ = 10/1 = 1 - verdien er dimensjonsløs. Her kan vi konkludere med at pliktsyklusen preger impulsen mye tydeligere enn pliktsyklusen.
Faktisk forble signalet det samme som i figur 9: en rektangulær puls med en amplitude på 1 V og en frekvens på 100 Hz. Bare fyllingsfaktoren eller pliktsyklusen er i endring, det er som om noen er mer kjent og praktisk. Men for å gjøre det lettere å observere i figur 10, er skanningens varighet halvert sammenlignet med figur 9 og er 1ms / div. Derfor tar signalperioden 10 celler på skjermen, noe som gjør det ganske enkelt å verifisere at driftssyklusen er 10%. Når du bruker et ekte oscilloskop, blir sveipens varighet valgt omtrent den samme.
Rektangulær måling av pulsspenning
Som nevnt i begynnelsen av artikkelen, måler oscilloskopet spenning, d.v.s. potensiell forskjell mellom to poeng. Typisk blir målinger foretatt i forhold til en vanlig ledning, jord (null volt), selv om dette ikke er nødvendig. I prinsippet er det mulig å måle fra minimum til maksimum signalverdier (toppverdi, topp til topp). I alle fall er måletrinnene ganske enkle.
Rektangulære pulser er ofte unipolare, noe som er typisk for digital teknologi. Hvordan måle spenningen til en rektangulær puls er vist i figur 11.
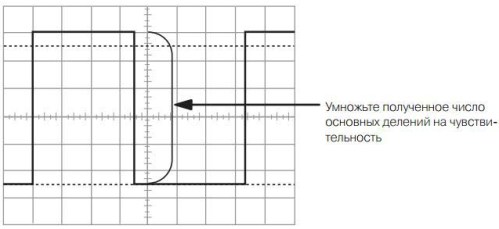
Figur 11. Måling av amplituden til en rektangulær puls
Hvis følsomheten til den vertikale avvikskanalen er 1V / div, viser det seg at figuren viser en puls med en spenning på 5,5V. Med en følsomhet på 0,1 V / div. Spenningen vil bare være 0,5V, selv om begge pulser på skjermen ser nøyaktig like ut.
Hva annet kan sees i en rektangulær impuls
De rektangulære pulser vist i figur 9, 10 er ganske enkelt ideelle fordi de er syntetisert av Electronics WorkBench. Og pulsfrekvensen er bare 100 Hz, derfor kan det ikke oppstå problemer med "kvissheten" i bildet. I en ekte enhet, med en høy repetisjonshastighet, er pulsen noe forvrengt, først av alt opptrer forskjellige bølger og utbrudd på grunn av installasjonsinduktansen, som vist i figur 12.
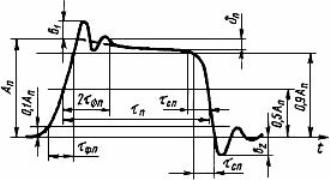
Figur 12. Real Rectangular Impuls
Hvis du ikke tar hensyn til slike "bagateller", ser den rektangulære impulsen ut som vist i figur 13.
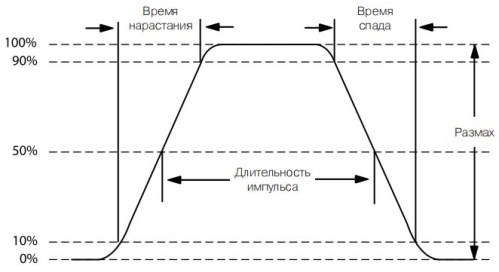
Figur 13. Parametere av en rektangulær puls
Figuren viser at pulsens for- og bakkanter ikke vises umiddelbart, men har noen stignings- og falltider, og er noe skrått i forhold til den vertikale linjen. Denne helningen skyldes frekvensegenskapene til mikrokretser og transistorer: jo høyere frekvenstransistor, jo mindre “fronter” på pulsen. Derfor bestemmes pulslengden av nivået 50% av hele området.
Av samme grunn bestemmes pulslens amplitude av nivået 10 ... 90%. Pulsens varighet, så vel som spenningen, bestemmes ved å multiplisere antall divisjoner av den horisontale skalaen med delingsverdien, som vist i figur 14.
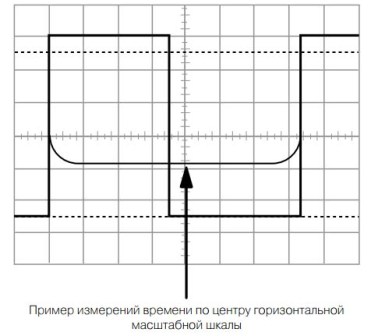
Figur 14
Figuren viser en periode med en rektangulær puls, litt forskjellig fra slynget: varigheten av en positiv puls er 3,5 divisjoner av den horisontale skalaen, og pausevarigheten er 3,8 divisjoner. Pulse repetisjonsperioden er 7,3 divisjoner. Et slikt bilde kan tilhøre flere forskjellige pulser med forskjellige frekvenser. Alt vil avhenge av varigheten av feien.
Anta en skanningsvarighet på 1 ms / div. Da er puls repetisjonsperioden 7,3 * 1 = 7,3 ms, som tilsvarer en frekvens på F = 1 / T = 1 / 7.3 = 0.1428KHz eller 143 Hz. Hvis skanningens varighet er 1 µs / div, vil frekvensen vise seg å være tusen ganger høyere, nemlig 143KHZ.
Ved å bruke dataene i figur 14, er det ikke vanskelig å beregne pulsens syklus for pulsen: S = T / τ = 7.3 / 3.5 = 2.0857, det viser seg nesten som en slingring. Driftssyklus plikt syklus D = τ / T = 3,5 / 7,3 = 0,479 eller 47,9%. Det skal bemerkes at disse parametrene på ingen måte er avhengige av frekvensen: pliktsyklus og driftssyklus ble bare beregnet av divisjoner på bølgeformen.
Med rektangulære impulser ser alt ut til å være klart og enkelt. Men vi glemte helt sinusbølgen. Det samme er faktisk: du kan måle spenninger og tidsparametere. En sinusbølgeperiode er vist i figur 15.
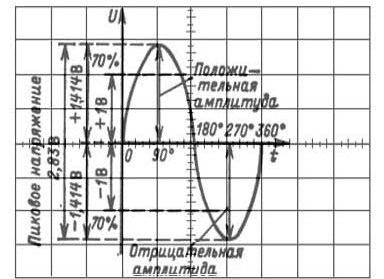
Figur 15. Sine Wave Parameters
For sinusformen vist på figuren er følsomheten til den vertikale avbøyningskanalen åpenbart 0,5 V / div. De gjenværende parametrene kan enkelt bestemmes ved å multiplisere antall divisjoner med 0,5V / div.
Sinusbølgen kan være en annen, som måles med følsomhet, for eksempel 5V / div. I stedet for 1V får du 10V. Imidlertid ser bildet av begge sinusoidene på skjermen nøyaktig det samme.
Tidspunktet for den viste sinusoid er ukjent. Hvis vi antar at skanningens varighet er 5ms / div, vil perioden være 20ms, som tilsvarer en frekvens på 50Hz. Tallene i grader på tidsaksen indikerer sinusoidens fase, selv om dette ikke er spesielt viktig for en enkelt sinusoid. Oftere er det nødvendig å bestemme faseskiftet (direkte i millisekunder eller mikrosekunder) minst mellom to signaler. Dette gjøres best med et tostråleoscilloskop. Hvordan dette gjøres vil bli vist nedenfor.
Hvordan måle strøm med et oscilloskop
I noen tilfeller er det nødvendig å måle strømens størrelse og form. For eksempel er vekselstrøm som strømmer gjennom en kondensator foran spenningen i ¼ periode. Deretter er en motstand med en liten motstand (tiendedeler av en Ohm) inkludert i åpen krets. Slik motstand påvirker ikke driften av kretsen. Spenningsfallet over denne motstanden vil vise formen og størrelsen på strømmen som strømmer gjennom kondensatoren.
Et lignende målerameter er anordnet på omtrent samme måte, som vil bli inkludert i brudd på den elektriske kretsen. I dette tilfellet er målemotstanden plassert inne i selve ammeteret.
Kretsen for å måle strømmen gjennom kondensatoren er vist på figur 16.
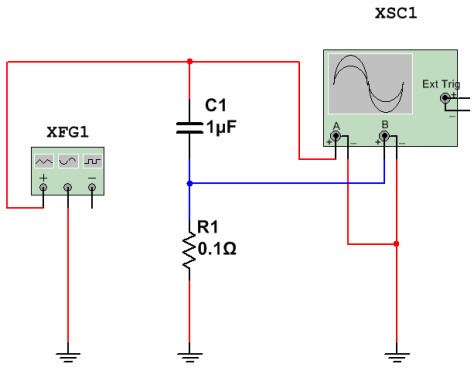
Figur 16. Strømmåling gjennom en kondensator
En sinusformet spenning på 50 Hz med en amplitude på 220 V fra XFG1-generatoren (rød stråle på oscilloskopskjermen) tilføres seriekretsen fra kondensatoren C1 og målemotstanden R1. Spenningsfallet over denne motstanden vil vise formen, fasen og størrelsen på strømmen gjennom kondensatoren (blå bjelke). Hvordan det vil se ut på oscilloskopskjermen er vist i figur 17.
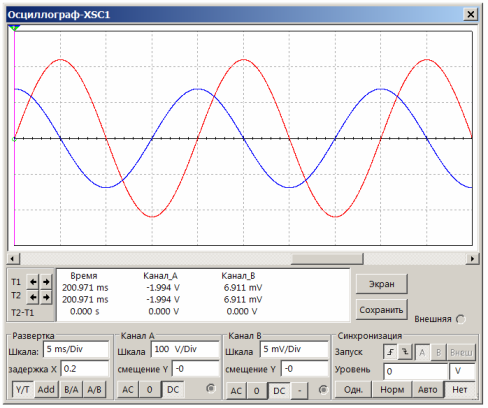
Figur 17. Strømmen gjennom kondensatoren er foran spenningen med ¼ periode
Ved en sinusbølgefrekvens på 50 Hz og en skanningstid på 5 ms / Div, tar en sinusbølgeperiode 4 divisjoner langs X-aksen, noe som er veldig praktisk for observasjon. Det er lett å se at den blå strålen ligger foran den røde med nøyaktig 1 divisjon langs X-aksen, som tilsvarer ¼ periode. Med andre ord, strømmen gjennom kondensatoren er foran fasespenningen, noe som er helt i samsvar med teorien.
For å beregne strømmen gjennom kondensatoren er det nok å bruke Ohms lov: I = U / R. Når målemotstanden er 0,1 Ohm, er spenningsfallet over den 7 mV. Dette er amplitudeverdien. Da vil maksimal strøm gjennom kondensatoren være 7 / 0,1 = 70 mA.
Å måle formen på strømmen gjennom kondensatoren er ikke noen veldig presserende oppgave, alt er klart og uten målinger. I stedet for en kondensator kan det være belastning: spole, motorvikling, transistorforsterkertrinn og mye mer. Det er viktig at denne metoden kan brukes til å studere strømmen, som i noen tilfeller skiller seg betydelig i form fra spenning.
Boris Aladyshkin
Se også på elektrohomepro.com
: