kategorier: Utvalgte artikler » Praktisk elektronikk
Antall visninger: 32001
Kommentarer til artikkelen: 2
Kondensatorer i elektroniske kretsløp
I tidligere artikler snakket vi kort om bruken av kondensatorer i vekselstrømskretser, hvordan og hvorfor kondensatorer passerer vekselstrøm (se - AC kondensatorer). I dette tilfellet varmes ikke kondensatorene opp, strømmen blir ikke tildelt dem: i den ene halvbølgen av sinusformen lader kondensatoren, og i den andre tømmer den seg naturlig ut, mens den lagrede energien overføres tilbake til strømkilden.
Denne metoden for å føre strøm lar deg kalle kondensatoren en fri motstand, og det er derfor kondensatoren som er koblet til uttaket ikke får telleren til å snurre. Og alt dette er fordi strømmen i kondensatoren er foran nøyaktig 1/4 av tiden spenningen som påføres den.
Men denne fasen fremskritt gjør det mulig ikke bare å "lure" telleren, men gjør det også mulig å lage forskjellige kretsløp, for eksempel generatorer av sinusformede og rektangulære signaler, tidsforsinkelser og forskjellige frekvensfiltre.
I prosessen med denne historien, vil det være nødvendig å huske noen ganger på det som allerede har blitt sagt før, for å si det slik, for å oppsummere. Dette vil hjelpe deg med å ikke gå tilbake til tidligere artikler for å huske en enkel formel, eller bare "hva er det?"
Parallell- og seriekobling av kondensatorer
Med en parallell tilkobling av kondensatorer er den totale kapasiteten ganske enkelt den aritmetiske summen av kapasitetene. Naturligvis, med denne inkluderingen, vil den totale kapasitansen være større enn kapasiteten til den største kondensatoren. Ctotal = C1 + C2 + C3 + ... + Cn.
Når det gjelder serieforbindelse, er den totale kapasiteten mindre enn den minste.
1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Når to identiske kondensatorer er koblet i serie, vil den totale kapasitansen være lik halvparten av kapasitansen til en: for eksempel når du kobler to kondensatorer på 1 uF hver, vil den totale kapasitansen være 0,5 uF.
Kapasitans Xc
Her er alt som mot tilkobling bare det motsatte: en seriekobling reduserer den totale kapasitansen, mens en parallell øker den. Denne omstendigheten skal ikke glemmes når du kobler til kondensatorer, siden en økning i kapasitansen fører til en reduksjon i kapasitansen Xc
Xc = 1/2 * π * f * C.
Fra matematikkens synspunkt er dette ganske naturlig, fordi kapasiteten C ligger i brøkdens nevner. Forresten, frekvensen f er på samme sted, så en økning i frekvensen fører også til en reduksjon i kapasitansen Xc. Den fysiske betydningen av dette er at gjennom den samme kondensatoren er det bedre, mer uhindret, at høye frekvenser passerer. Dette vil bli diskutert litt senere, når det gjelder lavpass- og høytpassfilter.
Hvis vi tar en kondensator med en kapasitet på 1 μF, vil Xc for en frekvens på 60 Hz være 2653 ohm, og for en frekvens på 400 Hz har den samme kondensatoren en Xc på bare 398 ohm. De som ønsker det kan sjekke disse resultatene med formelen ved å erstatte π = 3,14, frekvensen i hertz og kapasitansen i farader. Da blir resultatet i ohm. Alt må være i samsvar med SI-systemet!
Men kondensatorer brukes ikke bare som friddempende dempningsmotstand eller i likeretterfiltre. Uten deres deltakelse, kretsløp for lav- og høyfrekvente generatorer, forskjellige bølgeformomformere, differensierende og integrerende kretser, forsterkere og andre ordninger.
Deretter vil forskjellige elektriske signaler som kondensatorer må jobbe med bli vurdert. For det første er dette periodiske signaler som er egnet for observasjon med oscilloskop.
Periode og frekvens av svingninger
En periodisk svingning kalles derfor periodisk, som uten opphør gjentar den samme formen, for eksempel en sinusformet svingning. Varigheten av denne fullsvingen kalles nøyaktig perioden T, og måles i sekunder, millisekunder, mikrosekunder.Moderne elektronikk omhandler til og med nanosekunder (en milliarddel sekund).
Antall perioder per sekund kalles frekvensen (hvor ofte) av svingningene f, og uttrykkes i hertz. 1Hz er frekvensen som en svingning, en hel periode, utføres på 1 sekund. Forholdet mellom periode og frekvens uttrykkes med den enkle formelen T = 1 / f.
Følgelig, å kjenne til svingningsperioden, er det veldig enkelt å beregne frekvensen f = 1 / T.
Slik beregnes frekvensen når du måler med et oscilloskop: antall celler i en periode blir beregnet, multiplisert med varigheten til en celle, og perioden oppnås for eksempel i mikrosekunder. Og for å finne ut av frekvensen, brukte de ganske enkelt den siste formelen.
ordinære elektronisk oscilloskop Lar deg kun observere periodiske signaler som kan synkroniseres med sveipefrekvensen for å få et stillbilde som er egnet for forskning. Hvis du sender et signal til et musikkprogram til inngangen til oscilloskopet, vil du ikke kunne stoppe bildet for noe. For å observere slike signaler brukes lagringsoscilloskop.
Når en periode måles i millisekunder, oppnås frekvensen i kilohertz, i en periode målt i mikrosekunder, er frekvensen allerede uttrykt i megahertz. Dette er hvis du ikke følger SI-systemets krav: periode i sekunder, frekvens i hertz.
Ikke-sinusformede vibrasjoner
Som nevnt tidligere er en sinusbølge den vanligste og egner seg for studier og praktisk bruk av den periodiske kurven. Under industrielle forhold oppnås det ved bruk av elektriske generatorer, for eksempel i vannkraftverk. I elektroniske apparater brukes vibrasjoner av de mest forskjellige former.
I utgangspunktet er dette tre former: sinusformet, rektangulært og trekantet, som vist i figur 1. Både strøm og spenning kan ha en slik form, derfor viser figuren bare tidsaksen, ordinataksen blir stående uten navn.
Slike svingninger genereres av spesielle elektroniske kretsløp. Rektangulære og trekantede signaler kalles ofte pulserte. Imidlertid er det mange elektroniske kretsløp som utfører signalkonvertering: for eksempel et rektangel, en trekant kan lages av en sinus.
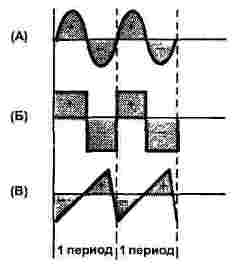
Figur 1
For alle tre signalene viser figuren to perioder, alle signaler har samme frekvens.
Spektrum av ikke-sinusformede signaler
Ethvert elektrisk signal kan fremstilles som en måling av amplituden på et eller annet tidspunkt. Frekvensen til disse prøvene kalles samplingsfrekvensen, og minst to ganger høyere enn den øvre frekvensen til det målte signalet. Deretter kan du gjenopprette det originale signalet fra disse prøvene. Denne metoden brukes for eksempel i digital lydopptak. Denne metoden kalles også tidsanalyse.
En annen metode forutsetter at ethvert signal, til og med rektangulært, kan representeres som den algebraiske summen av sinusoider med forskjellige frekvenser og faser. Denne metoden kalles frekvensanalyse. Men det som ble sagt "med forskjellige frekvenser" er ikke helt sant: de konstituerende sinusoidene kalles harmoniske og deres frekvenser overholder visse lover.
En sinusbølge hvis frekvens er lik frekvensen av en firkantbølge kalles den grunnleggende eller første harmoniske. Til og med harmonikker oppnås ved å multiplisere den grunnleggende frekvensen med et jevnt antall og henholdsvis oddetiske harmoniske med odde.
Så hvis den første harmonikken har en frekvens på 1000 Hz, så er den andre 2000 Hz, den fjerde er 4000 Hz, etc. Odd harmoniske vil ha frekvenser på 3000Hz, 5000Hz. Dessuten er hver harmonisk mindre i amplitude enn den viktigste: jo høyere harmonisk, jo mindre amplitude.
I musikk kalles harmoniske overtoner. Det er de som danner lydens klang, gjør det mulig å skille fiolinen fra pianoet og gitaren fra saksofonen. De tillater ikke å forvirre den mannlige og kvinnelige stemmen eller å skille Petrov fra Ivanov. Og bare bihulene i seg selv kan ikke lenger spaltes eller settes sammen fra noen signaler.
Figur 2 viser konstruksjonen av en rektangulær puls.
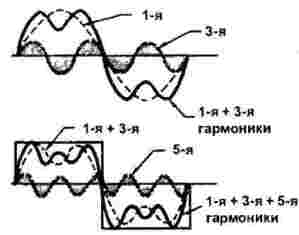
Figur 2
Den første og tredje harmonikken er vist i den øvre delen av figuren. Det er lett å se at i en periode av den første harmoniske tre perioder av tredje passering. I dette tilfellet er amplituden til den tredje harmonikken en tredjedel av den første. Summen av den første og tredje harmonikken vises også her.
Nedenfor, sammen med summen av 1 og 3 harmonier, vises ytterligere 5 harmonikker: for en periode med et rektangulært signal klarer det å gjøre nøyaktig fem perioder. I dette tilfellet er amplituden enda mindre, mer presist, nøyaktig 1/5 av den viktigste (første). Men man skal ikke tro at alt ender på den femte harmonien: det kan ganske enkelt ikke vises på figuren, faktisk er det mye mer.
Dannelsen av sagtann og trekantede signaler, vist i figur 3., er noe mer komplisert. Hvis det i forrige tilfelle bare rare harmonikker deltok, så kommer til og med harmoniske spill inn.
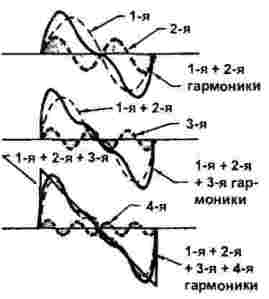
Figur 3
Dermed kan vi oppgi det faktum at ved hjelp av mange harmoniske syntetiseres et signal av enhver form, og antall og type harmoniske avhenger av bølgeformen, som vist i figur 2 og 3.
Ved reparasjon og montering av elektronisk utstyr brukes et oscilloskop for å studere elektriske signaler. Det lar deg vurdere formen av periodiske signaler, amplituden deres, måle repetisjonsperioden. Men harmonikkene vist i figur 2 og 3 kan ikke sees.
Selv om du for eksempel kobler en elektrisk gitar til et oscilloskop, drar i en streng, vises en sinus på skjermen, det er den første harmonien. I dette tilfellet kan det ikke være snakk om noen overtoner. Den samme bihulene vil oppstå hvis du blåser inn i røret eller fløyten foran mikrofonen.
Hvordan få rektangulære impulser
Etter å ha blitt kjent med elektriske signaler, må vi huske kondensatorene som artikkelen begynte med. Først av alt, bør du bli kjent med en av de klassiske elektronikkretsene - vibrator, (Figur 4) det er han som genererer rektangulære pulser. Kretsen er så klassisk at den begynner å fungere med en gang uten å kreve innstillinger eller justeringer.
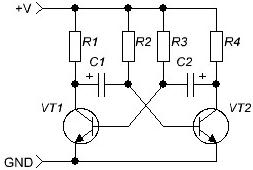
Figur 4
Multivibratoren er en totrinns forsterker, dekket av positive tilbakemeldinger. Hvis kollektorbelastningsmotstandene R1 = R4, basemotstandene R2 = R3 og kondensatorene C1 = C2 er like, kalles multivibratoren symmetrisk og genererer kvadratiske bølgepulser av slyngtypen - pulsens varighet er lik pausens varighet.
Pliktens syklus for slike pulser (forholdet mellom perioden og pulslengden) er lik to. I engelskspråklige ordninger er alt akkurat det motsatte: De kaller det plikt syklus. Det beregnes som forholdet mellom pulsvarighet og perioden etter suksess og uttrykkes som en prosentandel. Dermed er vikingssyklusen for meander 50%.
Er datamaskinen riktig?
Navnet multivibrator ble foreslått av den nederlandske fysikeren van der Pol, fordi spekteret til et rektangulært signal inneholder mange harmonikker. Du kan bekrefte dette hvis du kan plassere en radiomottaker som opererer i medium wave-området i nærheten av en multivibrator som fungerer selv med en lydfrekvens: hyl kommer fra høyttaleren. Dette antyder at multivibratoren i tillegg til lydfrekvens også avgir høyfrekvente svingninger.
For å bestemme generasjonsfrekvensen kan man bruke formelen f = 700 / (C1 * R2).
Med denne formen av formelen, kondensatoren til kondensatoren i mikrofarader (μF), motstanden i kilo-ohm (KΩ), resultatet i hertz (Hz). Dermed bestemmes frekvensen av tidskonstanten til C1 * R2-kretsen; samlerbelastninger påvirker ikke frekvensen. Hvis vi tar C1 = 0,02 μF, R2 = 39 KΩ, får vi f = 700 / (0,02 * 39) = 897,4 Hz.
Multivibrator i datamaskinens alder og mikrokontrollere I følge denne ordningen blir den nesten aldri brukt, selv om den godt kan være egnet for forskjellige eksperimenter. Først av alt, å bruke datamaskiner. Slik ser multivibratorkretsen samlet i Multisim-programmet ut. Forbindelsen til oscilloskopet er også vist her.
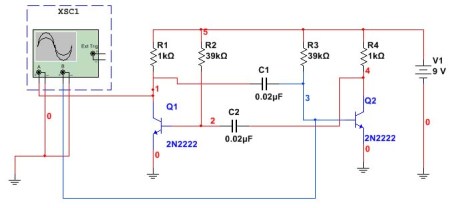
Figur 5
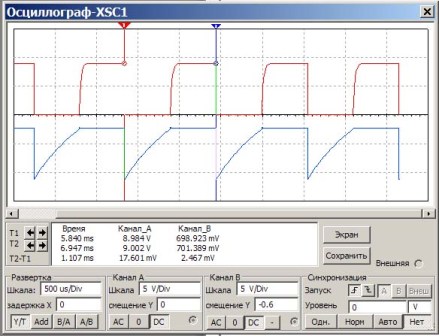
I denne kretsen er kondensatorer og motstander installert som i forrige eksempel. Oppgaven er å sjekke beregningen i henhold til formelen om samme frekvens vil oppnås. For å gjøre dette måler du pulsenes periode og beregner dem deretter på nytt. Resultatet av Multisim-oscilloskopet er vist i figur 6.
Figur 6
Noen presiseringer til figur 6.
På oscilloskopskjermen viser den røde pulsen pulsen på transistorsamleren, og den blå på basene. Under skjermen i et stort hvitt vindu viser tallene måleresultatene. Vi er interessert i kolonnen "Tid". Tiden måles med indikatorene T1 og T2 (røde og blå trekanter over skjermen).
Dermed er pulsrepetisjonstiden T2-T1 = 1.107ms vist ganske nøyaktig. Det gjenstår bare å beregne frekvensen f = 1 / T = 1 / 1,107 * 1000 = 903Hz.
Resultatet er nesten det samme som i beregningen i henhold til formelen, som er gitt litt høyere.
Kondensatorer kan ikke bare brukes separat: i kombinasjon med motstander lar de deg enkelt lage forskjellige filtre eller lage faseskiftkretser. Men dette vil bli diskutert i neste artikkel.
Fortsettelse av artikkelen: Kondensatorer i elektroniske kretsløp. Del 2
Boris Aladyshkin
Se også på elektrohomepro.com
: