Nåværende måling

DC strømmåling

I elektronisk teknologi er det ofte nødvendig å måle direkte strømmer. Tilsynelatende kan mange multimetre, for det meste billige, av denne grunn bare måle likestrøm. Måleområdet for vekselstrøm er i noen modeller av multimetre, som er dyrere, men disse indikasjonene kan bare klareres hvis strømmen har en sinusform og frekvensen ikke overstiger 50 Hz.

Krav til ammeter

Enhver måleenhet anses som god hvis den ikke fører til forvrengninger i den målte mengden, eller rettere sagt introduserer, men så lite som mulig. For et voltmeter er dette en høy inngangsimpedans, siden den er koblet parallelt med en del av kretsen. Det er hensiktsmessig å minne om at med en parallell forbindelse, reduseres den totale motstanden til seksjonen.

Ammeter er inkludert i kretsbruddetDerfor anses en positiv kvalitet, i motsetning til et voltmeter, for å være bare en lav indre motstand. Dessuten, jo mindre er jo bedre, spesielt når du måler lave strømmer, så iboende i elektroniske kretsløp. Gjeldende måleprosess er vist på figur 1.

Diagrammet viser en enkel elektrisk krets bestående av et galvanisk batteri og to motstander, bare egnet for å utføre eksperimenter på måle strømmer. Først av alt, bør du ta hensyn til enhetens polaritet, det må sammenfalle med strømretningen, som er indikert med piler.

Figuren viser en pekerenhet som ikke vil vises i motsatt retning. For et digitalt multimeter betyr ikke strømmen. Hvis den er koblet feil, vil den ganske enkelt vise et minustegn, og konflikten blir avgjort på dette. Matematikere vil si at modulet til et tall er målt, det ser ut som det er navnet på det usignerte tallet.

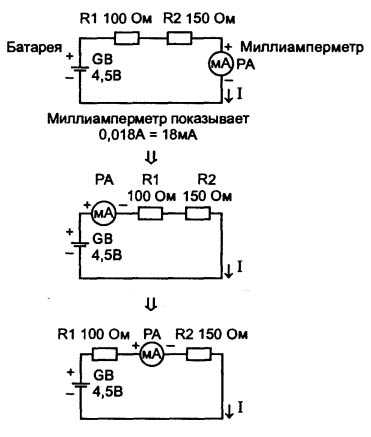
Figur 1Nåværende måleprosess

Hva ammeteret vil vise

For en så enkel krets er det ikke vanskelig å beregne strømmen, den vil være 0,018A eller 18mA. Samtidig viser figuren at en milliammeter i samme krets er koblet på tre forskjellige punkter. I følge fysikkens lover vil avlesningene hans være nøyaktig de samme, fordi hvor mange elektroner som "strømmer ut" fra plusset til batteriet, returnerer det samme tallet tilbake, men etter et "minus". Og banen for alle disse elektronene er den samme: disse er tilkoblingsledninger, motstander, og hvis tilkoblet, da millimeter.

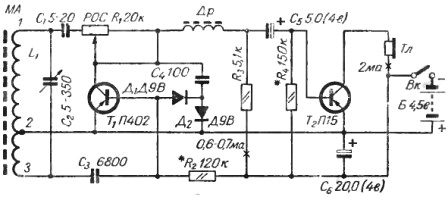
Figur 2 viser et diagram av en to-transistor-mottaker fra boken til M.M. Rumyantsev "50 kretser av transistormottakere" (1966).

Figur 2Dual Transistor mottakerkrets

I disse dager ble kretser i bøker ledsaget av detaljerte beskrivelser og metoder for justering av dem. Det ble ofte anbefalt å måle strømmer i spesifikke deler av kretsen, vanligvis kollektorstrømmene til transistorer. Steder for måling av strømmer ble vist på diagrammet med et kryss. På dette tidspunktet var selvfølgelig en milliammeter koblet til spalten i lederen, og ved å velge verdien av motstanden merket med en stjerne, ble strømmen som ble indikert umiddelbart på diagrammet valgt.

Fallgruver i måling av strømmer

Figur 3 og 4 viser den enkleste kretsen, et batteri, en motstand og en multimeter. I følge Ohms lov er det lett å beregne at strømmen i denne kretsen vil være

I = U / R = 1,5 / 10 = 0,15A eller 150 mA.

Hvis du ser nøye på begge figurene, viser det seg at avlesningene på enhetene er forskjellige, selv om ingenting har endret seg i selve ordningene, hvis de kan kalles det. I figur 3 er målingene helt i samsvar med Ohms beregning.

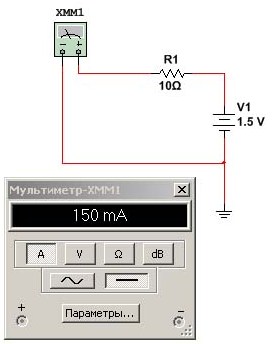
Figur 3. Målinger strøm i programsimulatoren Multisim

Men i figur 4 ble de litt lavere, nemlig 148,515mA. Spørsmålet er, hvorfor? Tross alt har ingenting endret seg på kretsen, kilden er den samme og motstanden har ikke blitt mer eller mindre.

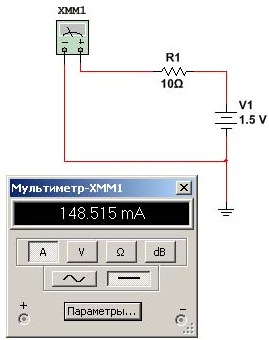
Figur 4. Målinger strøm i programsimulatoren Multisim

Faktum er at multimeterets egenskaper kan endres, noe som gjøres ved å klikke på "Alternativer" -knappen.I dette tilfellet ble ampeterens inngangsmotstand endret: i figur 3 var den 1n & # 8486; og i figur 4 ble den økt til 100mΩ, eller bare 0,1Ω. Dette eksemplet er gitt for å demonstrere hvordan egenskapene til et måleinstrument påvirker resultatet. I dette tilfellet en ammeter.

La oss prøve å øke strømmen 10 ganger i denne kretsen. For å gjøre dette er det nok å redusere motstandens verdi også med 10 ganger, da er det lett å beregne at amperemet vil vise halvannen ampère. Hvis inngangsimpedansen er 1nΩ, som i figur 3, vil resultatet være 1,5A, noe som er helt i samsvar med Ohms beregning.

Hvis du bruker ovennevnte knapp “Parametere” for å gjøre motstanden til ampermeteret 0,1Ω, kan du på skalaen til enheten se 1 364A. Selvfølgelig er 0.1Ω litt for stor for et ekte ammeter, og 1nΩ skjer sannsynligvis bare i programmet - simulatoren kan fremdeles se hvordan den interne motstanden til enheten påvirker måleresultatet. Generelt, for å gjøre slike målinger, må man umiddelbart finne ut "i sinnet" i det minste rekkefølgen på resultatet. Men du bør starte med et åpenbart større utvalg på enheten.

Dette er tilfelle når du måler strømmer i et simulatorprogram, der alt bevisst er satt for å oppnå bedre resultater. Alle deler med minimale toleranser, inngangsimpedansene til enhetene er også ideelle, omgivelsestemperaturen er 25 grader. Men som nettopp vist, parametrene til enheter, deler og jevn temperatur kan stilles inn på forespørsel fra brukeren.

Målinger med dette instrumentet

I det virkelige liv er alt ikke så glatt. Brede motstander kan ha toleranser på som regel ± 5, 10 og 20 prosent. Selvfølgelig er det motstander med toleranser på en tidels prosent, men de brukes bare der det virkelig er nødvendig, og ikke i det hele tatt i utstrakt bruk utstyr i nærheten av hver transistor og i nærheten av hver mikrokrets.

Det antas at eksperimenter på måling av strømmer utføres med motstander med en 5% toleranse. Da, til den nominelle verdien (det som står skrevet på motstandskassen), for eksempel 10KΩ, kan en motstand med en motstand i området 9,5 ... 10,5KΩ falle under armen. Hvis en slik motstand er koblet til en spenningskilde, for eksempel 10V, kan du når du måler strømmer få verdier i området 1.053 ... 0.952mA, i stedet for den forventede 1mA. En enda større spredning vil oppnås når du bruker motstander med en toleranse på 10 eller 20 prosent.

Og helt fantastiske resultater kan oppnås hvis disse eksperimentene utføres på batteristrøm. Kretsen er nøyaktig den samme som på figur 3 og 4. Den er så enkel at du helt kan avgi lodding og trykte kretskort, gjøre alt bare med vendinger, eller bare holde det i hendene.

La oss estimere hva som skal vise seg, hva enheten skal vise. Det er kjent at batterispenningen er 1,5V, motstand 10Ω. I følge Ohms lov er jeg = U / R = 1,5 / 10 = 0,15A eller 150mA.

I faktiske målinger, i stedet for de forventede 150 mA, viste enheten 98,3 mA. Selv om vi antar at motstanden er fanget med en 20 prosent toleranse, er I = U / R = 1,5 / 12 = 0,125A eller 125 mA.

Det blir ikke nok! Hvor ble det av? I vårt tilfelle viste det "døde" batteriet seg å ha skylden. Under operasjonen mistet hun deler av siktelsen, og hennes interne motstand økte. Ved å legge til den ytre motstandens motstand, ga den interne motstanden sitt "bidrag" til forvrengningen av måleresultatet. Det var disse omstendighetene som førte til at apparatets målinger mildt sagt var veldig langt fra de forventede.

Derfor, når man måler i elektroniske kretsløp, må man være ekstremt forsiktig, nøyaktigheten vil heller ikke være overflødig. Kvaliteter som er direkte motsatt av de nettopp nevnte fører til katastrofale resultater. Måleinstrumenter kan brennes, apparater som utvikles eller repareres også, og i noen tilfeller til og med få et elektrisk støt. For å unngå skuffelse fra slike tilfeller, kan vi nok en gang anbefale tilbakekalling forholdsregler.

Boris Aladyshkin