kategorier: Praktisk elektronikk, Apparatreparasjon
Antall visninger: 26598
Kommentarer til artikkelen: 2
Spenningsmåling
I amatørradiopraksis er dette den vanligste målingstypen. For eksempel, når du reparerer en TV, måles spenninger ved karakteristiske punkter på enheten, nemlig ved terminalene til transistorer og mikrokretser. Hvis du har for hånden et kretsskjema, og det viser modusene for transistorer og mikrokretser, vil det ikke være vanskelig for en erfaren master å finne en funksjonsfeil.
Når man bygger selvmonterte strukturer, kan man ikke fjerne stresmåling. Unntak er bare klassiske ordninger, som de skriver noe sånt om: "Hvis designen er satt sammen fra serviceverdige deler, er det ikke nødvendig med noen justering, det vil fungere med en gang."
Som regel er dette klassiske elektroniske kretsløp, for eksempel vibrator. Den samme tilnærmingen kan oppnås selv for en lydfrekvensforsterker, hvis den er montert på en spesialisert brikke. Som et godt eksempel er TDA 7294 og mange flere sjetonger i denne serien. Men kvaliteten på de "integrerte" forsterkerne er liten, og ekte kjennere bygger sine forsterkere på diskrete transistorer, og noen ganger på elektroniske rør. Og her er det bare det du ikke kan gjøre uten å justere og relaterte stressmålinger.
Hvordan og hva du skal måle
Vist i figur 1.
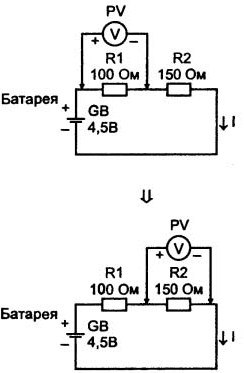
Figur 1
Kanskje noen vil si, de sier, hva kan måles her? Og hva er vitsen med å sette sammen en slik kjede? Ja, det er nok vanskelig å finne praktisk anvendelse for en slik ordning. Og for pedagogiske formål er det ganske passende.
Først av alt, bør du ta hensyn til hvordan voltmeteret er tilkoblet. Siden DC-kretsen er vist på figuren, er voltmeteret koblet i samsvar med polariteten som er angitt på enheten i form av pluss- og minustegn. I utgangspunktet stemmer denne merknaden for pekerenheten: hvis polariteten ikke blir observert, vil pilen avvike i motsatt retning, i retning av nulldelingen av skalaen. Så vi får en slags negativ null.
Digitale enheter, multimeter, i denne forbindelse er mer demokratiske. Selv om test sonder koblet i omvendt polaritet, vil spenningen fortsatt måles, bare et minustegn vises på skalaen før resultatet.
En annen ting å merke seg når du måler spenninger er måleområdet for enheten. Hvis den estimerte spenningen er i området for eksempel 10 ... 200 millivolt, tilsvarer skalaen til enheten 200 millivolt, og det er usannsynlig å måle spenningen i en skala på 1000 volt for å gi et forståelig resultat.
Du bør også velge et måleområde i andre tilfeller. For en målt spenning på 100 volt er et område på 200V og til og med 1000V ganske passende. Resultatet blir det samme. Det når det gjelder moderne multimeter.
Hvis målingene gjøres av den gode gamle pekerenheten, må du velge måleområdet når målingene er midt i skalaen, for å måle spenningen på 100V, noe som gir mulighet for en mer nøyaktig avlesning.
Og en mer klassisk anbefaling om bruk av et voltmeter, nemlig: hvis størrelsen på den målte spenningen er ukjent, bør målingene startes ved å sette voltmeteret til det største området. Hvis den målte spenningen er 1V, og rekkevidden er 1000V, er faktisk den største faren ved feil måling av enheten. Hvis det viser seg det motsatte, er måleområdet 1V, og den målte spenningen er 1000, å kjøpe en ny enhet kan ganske enkelt ikke unngås.
Hva et voltmeter vil vise
Men kanskje kommer vi tilbake til figur 1, og prøver å finne ut hva begge voltmetere vil vise. For å bestemme dette, må du gjøre det dra nytte av Ohms lov. Problemet kan løses i noen få trinn.
Beregn først strømmen i kretsen. For å gjøre dette, er det nødvendig å dele kildespenningen (på figuren er det et galvanisk batteri med en spenning på 1,5 V) av kretsmotstanden.Med en seriekobling av motstander vil dette ganske enkelt være summen av motstandene deres. I form av en formel ser det ut slik: I = U / (R1 + R2) = 4.5 / (100 + 150) = 0.018 (A) = 180 (mA).
En liten merknad: hvis uttrykket 4,5 / (100 + 150) er kopiert til utklippstavlen, deretter limt inn i vinduet til Windows-kalkulatoren, vil du etter å ha trykket på "lik" -tasten oppnå resultatet av beregningene. I praksis beregnes enda mer komplekse uttrykk som inneholder firkantede og krøllete seler, grader og funksjoner.
For det andre, få måleresultatene, som spenningsfallet over hver motstand:
U1 = I * R1 = 0,018 * 100 = 1,8 (V),
U2 = I * R2 = 0,018 * 150 = 2,7 (V),
For å bekrefte korrektheten av beregningene er det nok å legge til begge resulterende verdier på spenningsfallet. Summen må være lik batterispenningen.
Kanskje noen kan spørre: “Og hvis skillet ikke kommer fra to motstander, men fra tre eller til og med fra ti? Hvordan bestemme spenningsfallet på hver av dem? " På samme måte som i det beskrevne tilfellet. Først må du bestemme kretsens totale motstand og beregne den totale strømmen.
Deretter blir denne allerede kjente strømmen ganske enkelt multiplisert med motstand fra den korresponderende motstanden. Noen ganger må du gjøre slike beregninger, men det er en ting også. For ikke å tvile på resultatene som er oppnådd, bør strømmen i formlene erstattes med Amperes, og motstanden i Ohms. Da blir resultatet uten tvil i Volts.
Voltmeter inngangsimpedans
Nå er alle vant til å bruke kinesiske enheter. Men dette betyr ikke at kvaliteten deres er ubrukelig. Det er bare det at i Russland var det ingen som tenkte på å produsere sine egne multimeter, og piletesterne glemte tilsynelatende hvordan de skulle gjøre det. Bare synd for staten.
Fig. 2. MultimeterDT838
En gang i tiden indikerte instruksjonene for instrumentene deres tekniske egenskaper. Spesielt for voltmetre og brytertestere var dette inngangsmotstanden, og det ble angitt i kilo ohm / volt. Det var enheter med en motstand på 10 K / V og 20 K / V. De sistnevnte ble ansett som mer nøyaktige, siden den målte spenningen ble redusert mindre og viste et mer nøyaktig resultat. Ovennevnte kan bekreftes av figur 3.
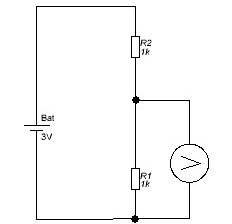
Figur 3
Figuren viser spenningsdelere av to motstander. Motstanden til hver motstand er 1KΩ, forsyningsspenningen er 3V. Det er lett å gjette, selv det ikke er nødvendig å vurdere noe, at på hver motstand vil det være nøyaktig halve spenningen.
Tenk deg nå at målingene blir utført av TL4-enheten, som i spenningsmålsmodus har en inngangsimpedans på 10KΩ / V. Ved spenningen som er indikert i diagrammet, er målegrensen på 3V ganske passende, hvor voltmeterens totale motstand vil være 10 * 3 = 30 (KOhm).
Dermed viser det seg at ytterligere 30KΩ er koblet parallelt med motstanden med en motstand på 1KΩ. Da vil den totale motstanden når den er koblet parallelt være 999.999 Ohm. Selv om det er noe mindre, men ikke så mye. Derfor vil feilen i spenningsmåleresultatet være ubetydelig.
Hvis begge motstandene til skillelinjen har en nominell verdi på 1 megaohm, vil beregningsresultatene se slik ut:
Den totale motstanden til et parallelt tilkoblet voltmeter og motstand R1 vil være mindre enn mindre, og ved beregning vil den være 29.126KΩ. Den som ikke tror, kan for praksis beregne på nytt i henhold til formler for parallell forbindelse av motstander.
Total strøm i delekretsen: I = U / (R1 + R2) = 3 / (1000 + 29.126) = 0,0029150949446423470012418304464176 (mA).
Motstandsverdiene er erstattet i kilo-ohm, så strømmen viste seg i milliamp. Så viser det seg at voltmeteret vil vise seg
0,0029150949446423470012418304464176 * 29.126 ≈ 0,085 V.
Og halvparten var forventet, d.v.s. halvannen volt! Hvis strømmen er i milliamper, er motstanden i kilo-ohm, og resultatet oppnås i volt. Selv om de ikke er i henhold til SI-systemet, gjør de det noen ganger.
En slik skillelinje er selvfølgelig noe urealistisk: hvorfor sette motstander med en motstand på 1 megohm ved en spenning på bare 3V? Eller kanskje brukes en slik skillelinje et sted, bare spenningen på den må måles med en helt annen enhet.
For eksempel har en av de billigste kinesiske multimetrene DT838, på alle spenningsmåleområder, en inngangsmotstand på 1 megohm, mye høyere enn enheten i forrige eksempel. Men dette betyr overhode ikke at pilemålerne har overlevd alderen. I noen tilfeller er de rett og slett uerstattelige.
Måling av vekselstrøm
Alle metoder og anbefalinger relatert til måling av konstant spenning er også gyldige for variabler: voltmeteret er koblet parallelt med kretsseksjonen, inngangsmotstanden til voltmeteret skal være så stort som mulig, måleområdet skal tilsvare den målte spenningen. Men når du måler vekslende spenninger, bør ytterligere to faktorer tas med i betraktningen, som konstant spenning ikke har. Dette er spenningsfrekvensen og dens form.
Målinger kan utføres av to typer enheter: enten et moderne digitalt multimeter, eller en "antediluviansk" peker-tester. Begge enhetene i denne målingen er naturlig nok inkludert i måling av vekslende spenninger. Begge enhetene er designet for å måle spenningen til en sinusform, og vil samtidig vise det rms verdi.
Den effektive spenningen U er 0,707 for amplitudespenningen Um.
U = Um / √2 = 0,707 * Um, hvorfra det kan konkluderes at Um = U * √2 = 1,41 * U
Et gjennomgripende eksempel er passende her. Ved måling av AC spenning viste enheten 220V, noe som betyr at amplitudeverdien i henhold til formelen er
Um = U * √2 = 1,41 * U = 220 * 1,41 = 310V.
Denne beregningen bekreftes hver gang nettstrømmen blir utbedret av en diodebro, hvoretter det er minst en elektrolytisk kondensator: hvis du måler konstant spenning ved broutgangen, vil enheten vise bare 310V. Dette tallet må huskes, det kan være nyttig i utvikling og reparasjon av bytte strømforsyninger.
Den angitte formelen er gyldig for alle påkjenninger hvis de har en sinusform. For eksempel, etter en trapp ned transformator er det en 12 V bytte. Så, etter å ha rettet ut og glattet ut kondensatoren, får vi
12 * 1,41 = 16,92 nesten 17V. Men dette er hvis belastningen ikke er tilkoblet. Når lasten er tilkoblet, vil likespenningen falle til nesten 12V. I tilfelle når spenningsformen er annerledes enn sinusbølgen disse formlene ikke fungerer, viser ikke enhetene hva som var forventet av dem. Ved disse spenningene utføres målinger av andre instrumenter, for eksempel et oscilloskop.
En annen faktor som påvirker voltmeteravlesningene er frekvensen. For eksempel måler DT838 digitale multimeter vekslende spenninger i frekvensområdet 45 ... 450 Hz, i henhold til dets egenskaper. Litt bedre i denne forbindelse er den gamle TL4-pekertesteren.
I spenningsområdet opp til 30V er frekvensområdet 40 ... 15000Hz (nesten hele lydområdet kan brukes når du stiller inn forsterkere), men med økning i spenning reduseres den tillatte frekvensen. I 100V-serien er den 40 ... 4000Hz, 300V 40 ... 2000Hz, og i 1000V-rekkevidden er den bare 40 ... 700Hz. Her er en udiskutabel seier over en digital enhet. Disse tallene gjelder også bare for sinusformede belastninger.
Selv om det noen ganger ikke er nødvendig med data om formen, frekvensen og amplituden til de vekslende spenningene. Hvordan kan du for eksempel bestemme om den lokale oscillatoren til en kortbølgemottaker fungerer eller ikke? Hvorfor “mottar” ikke mottakeren noe?
Det viser seg at alt er veldig enkelt, hvis du bruker en pekerenhet. Det er nødvendig å slå den på til en hvilken som helst grense for måling av vekslende spenninger og med en sonde (!) Berør terminalene til den lokale oscillatortransistoren. Hvis det er høyfrekvente svingninger, blir de oppdaget av diodene inne i enheten, og pilen vil avvike til en del av skalaen.
Se også på elektrohomepro.com
: