Boolsk algebra. Del 1. Litt historie

På skolen studerte vi alle algebra, men de snakket ikke om boolsk algebra der. Hva er forskjellen mellom boolsk algebra og skolealgebra, historien til dens utseende, problemer og anvendelser er beskrevet i denne artikkelen.

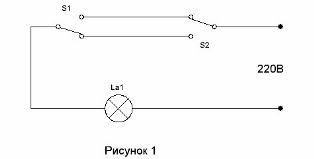
Kretsen som lar to brytere slå på lyset i korridoren ved inngangen til korridoren og slå det av når du kommer inn i rommet har vært kjent i veldig lang tid (se. Korridor for belysningskontroll). Det er vist på figur 1.

Oppgave nummer 1. Mer komplisert. Lag et diagram som lar deg slå av og på lyset på rommet ditt med en av tre forskjellige brytere. Brytere er plassert ved inngangen til rommet, over sengen og på pulten.

Oppgave nummer 2.

I et idrettsutvalg, for eksempel et fabrikkutvalg, samlet 5 dommere.

Hver av dem må stemme for forskjellige beslutninger. Avgjørelsen blir vedtatt med et flertall av stemmene, men bare under tilleggsbetingelsen at leder av komiteen stemmer for det.

Dommerne stemmer ved å trykke på knappen som lukker bryteren som ligger under bordet der de sitter. Lukker bryteren, stemmer de for og kobler ulempene. Tegn et enkelt diagram som lar deg automatisk se avstemmingsresultatene. I det enkleste tilfelle, ganske enkelt ved hjelp av en lyspære - tent - avgjørelsen ble tatt, lyste ikke opp - nei.

Oppgave nummer 3. I praksis er dette lite sannsynlig, men som en kompleks pedagogisk oppgave er ganske passende.

I et stort sekskantet rom er det installert en bryter på hver vegg. Bygg en krets slik at du når som helst kan slå på eller slå av lyset i rommet ved å vri en (hvilken som helst) bryter.

Etter at du uten hell har sittet over oppgaver i tre til fire dager, må du legge dem til side midlertidig. Og bli opptatt Boolsk algebra. Det er boolsk algebra, eller som det også kalles, Boolsk algebra, relékretsalgebra, vil hjelpe deg med å løse dine problemer.

Hva er boolsk algebra?

Merkelig nok, til tross for at de i fem år har studert algebra på skolen, vil mange elever og senere voksne ikke kunne svare på spørsmålet, hva er algebra? Algebra er en vitenskap som studerer settene til noen elementer og handlingene på dem.

På et skolekurs i algebra er slike elementer tall. Tall kan betegnes ikke med tall, men med bokstaver, alle er kjent med dette. I de første leksjonene i algebra gjør dette det alltid vanskelig for mange studenter. Husk hvor vanskelig det først var å bli vant til å legge bokstaver i stedet for tall, løse ligninger som ikke sier noe.

Sannsynligvis stilte hver av oss oss da spørsmålet: "Hvorfor trenger vi å oppgi bokstaver i stedet for tall, og er det i det hele tatt nødvendig?" Og først senere så du hvilke fordeler algebra gir når du løser problemer i forhold til aritmetikk.

Algebra brukes i mange eksakte vitenskaper. Dette er fysikk, mekanikk, sopromat, elektrisitet. Ohms lov det er ikke noe mer enn en algebraisk ligning: det er nok å erstatte deres numeriske verdier i stedet for bokstaver for å finne ut hvilken strøm som vil strømme i belastningen, eller hvilken motstand en del av kretsen har.

Så du ble kjent med algebra av tall, eller med elementær algebra. Den viktigste og nesten unike oppgaven er å få et svar på spørsmålet: “Hva er X lik? Hvor mye? ”

På videregående studerer de begynnelsen av vektoralgebra. Denne algebra er grunnleggende forskjellig fra elementær algebra. Det har en annen karakter av det studerte settet og andre handlingsregler. Løsning av vektorligningen får vi i svaret en vektor som ikke er et vanlig tall som svarer på spørsmålet "Hvor mye?"

Formlene for vektoralgebra er på mange måter forskjellige fra formlene for elementær algebra. For eksempel, i elementær algebra og i vektoralgebra er det en tilleggsoperasjon. Men det utføres på helt andre måter.Tilsetningen av tall er slett ikke den samme som tilsetningen av vektorer.

Det er andre algebraer: lineær algebra, algebra av strukturer, algebra av ringer, algebra av logikk, eller, hva er det samme, boolsk algebra. Du hørte sannsynligvis ikke navnet i skoletimene. George Boole - men alle vet navnet til en av hans talentfulle døtre Ethel Voinich (1864 - 1960). Hun skrev romanen "Gadfly", som forteller om kampen for rettighetene til italienske karbonister.

George Bull ble født i England 2. november 1815. Hele livet jobbet han som lærer i matematikk og fysikk på skolen. Fra memoarene til studentene hans er det kjent hvilken stor betydning Bul la til utviklingen av studentenes kreative evner. Da han presenterte nytt materiale, prøvde han å sikre at studentene selv "oppdaget" bestemte formler og lover.

Når han fortalte elevene om vanskene som vitenskapsmenn uunngåelig møtte i jakten på sannhet, likte læreren å gjenta en østlig visdom: selv den persiske tronen kan ikke gi så stor glede for en person som den minste vitenskapelige oppdagelsen. Buhl mistet aldri håpet om at en dag studentene hans skulle gjøre en virkelig oppdagelse.

Utvalget av vitenskapelige interesser fra Buhl var veldig bredt: Han var like interessert i matematikk og logikk - vitenskapen om lover og tanker. I disse dager ble logikk betraktet som en humanistisk vitenskap, og mange som kjente George Boole var overrasket over hvordan de eksakte metodene for kognisjon som er iboende i matematikk og rent beskrivende metoder for logikk, kunne eksistere sammen i en person.

Men forskeren ønsket å gjøre vitenskapen om lover og tenkningsformer like strenge som noen av naturvitenskapene, sier matematikk og fysikk. For å gjøre dette begynte Boule å betegne ikke tall som bokstaver, slik det gjøres i vanlig algebra, men utsagn og viste at slike ligninger, veldig lik algebraiske, kan løse spørsmål om sannheten og falskheten i uttalelser fra mennesket. Så den boolske algebra oppsto.

Men lenge før George Buhl kom den tyske matematikeren og filosofen Gottfried Leibniz (1646-1716) først på ideen om å lage en vitenskap som skulle utpeke alle begrepene vanlig ordetale tale med symboler og etablere noen ny algebra for å kombinere disse symbolene.

Etter opprettelsen av en slik vitenskap, vil ifølge Leibniz, forskere og filosofer slutte å krangle og rope på hverandre, finne ut sannheten, men de vil plukke opp en blyant og rolig si: "La oss beregne!"

I dag har algebraen til logikk blitt en viktig del av matematikken. En av oppgavene er å løse alle slags ligninger, hvis numeriske forhold er erstattet av alfabetiske. Hver av dere husket sannsynligvis gjennom hele livet hvordan man løste ligninger av andre og tredje grad med bokstavkoeffisienter. Så Boole i sin nye algebra brukte alle disse formlene og reglene.

Det som er nytt i den boolske algebraen er at elementene i settet som studeres i den ikke er tall, men utsagn. Hvis det løses vanlige algebraiske ligninger når det blir bestemt hvilket antall som tilsvarer ukjent X, søker skolealgebra svaret på spørsmålet: "Hvor mye?"

Logikkens algebra leter etter svaret på spørsmålet: "Er denne eller den uttalelsen betegnet med bokstaven X sann?"

Betydningen og innholdet i utsagnet spiller ikke noen rolle her. Hver uttalelse kan bare være sann eller usann. Det kan ikke være halvt sant og halvt usant. Som et eksempel kan vi huske at vi kastet masse med en mynt.

Bare to myntstater blir vurdert der - hoder eller haler. Etter avtale med partene er ørnen JA, og halene er NEI. Ingen andre mellompoeng tas med i sannsynlighetsteorien, selv om de er mulige. En vendt mynt kan falle på en kant, rulle ned gulvet til bena på en stol eller et bord og forbli i en oppreist stilling, eller til og med falle i et bredt gap i gulvet. (I analogi med elektriske kretsløp kan de to siste situasjonene betraktes som en funksjonsfeil i form av en brent kontakt).Men i disse dager ble boolsk algebra, dessverre, ikke mye brukt.

Claude Shannon "oppdaget" Buhl-algebra igjen. I 1938, mens han fremdeles var student ved Massachusetts Institute of Technology and America, beviste den unge Claude at den boolske algebraen er helt egnet for analyse og syntese av relé og switching kretsløp.

Ved hjelp av boolsk algebra er det veldig enkelt å lage en elektrisk krets av en automat som fungerer på et relé.For dette viser det seg, du trenger bare å vite nøyaktig hva maskinen skal gjøre, det vil si at du trenger å ha en algoritme for dens drift. Så grunnlaget ble lagt for teorien om digitale maskiner som opererer etter prinsippet JA eller NEI.

Slik i korte trekk er historien til den boolske algebraen. I de følgende artiklene vil vi vurdere de grunnleggende lovene, eksempler på kontaktkretser som implementerer disse lovene. Vurder løsningen på oppgavene som ble gitt i begynnelsen av artikkelen.

Fortsettelse av artikkelen: Boolsk algebra. Del 2. Grunnleggende lover og funksjoner

Boris Aladyshkin