Boolsk algebra. Del 2. Grunnleggende lover og funksjoner

Fortsettelse av historien om boolsk algebra, konvensjoner, regler, operasjoner. Gå til det grunnleggende om kontaktkretser.

den første artikkel George Bull ble beskrevet som skaperen av algebra av logikk. Den andre artikkelen vil beskrive de grunnleggende operasjonene av boolsk algebra, og metoder for å forenkle boolske uttrykk. Altså, boolesk algebra bruker utsagn som argumenter, og ikke deres betydning, men sannheten eller usannheten i utsagnet.

Skjemaet for å skrive uttrykk i boolsk algebra.

Hvis utsagnet er sant, er det skrevet slik: A = 1, hvis det er usant, så er A = 0 (det er tross alt ikke sant at potet er en frukt). For enhver uttalelse er A enten sant (A = 1) eller usant (A = 0). Det kan ikke være noen midt her. Vi har allerede snakket om dette.

Hvis du kobler to enkle uttalelser med forbundet Og, får du et sammensatt utsagn, som kalles et logisk produkt. La oss ta to enkle ordtak: “Tre er mer enn to” vil vi utpeke med bokstav A, “Tre mindre enn fem” - med bokstav B.

Derfor er den sammensatte uttalelsen “Tre er mer enn to Og mindre enn fem” en logisk (i dette tilfellet, bokstaven og, sier at dette er en "OG" logisk operasjon, så vel som senere i teksten "ELLER" og "IKKE.") og B. Det betegnes som følger: A ^ B eller A * B.

Logisk multiplikasjon (operasjon "OG").

I elementær algebra A * A = A2. Men i Buhls algebra A * A = A2 = A, A * A = A, siden multiplikasjonstegnet (*) nå betyr ... Og ... i betydningen And ... And. All vår erfaring bekrefter at A&A er den samme som A. alene. Man kan ikke være uenig i dette. Uttalelsens sannhet endres ikke hvis den gjentas av faktoren flere ganger.

Produktet fra to utsagn anses som sant (lik 1), da, og bare hvis begge faktorene er sanne, og usanne (lik 0) hvis minst en av faktorene er usanne. Enig i at disse reglene ikke er i strid med sunn fornuft, og at de i tillegg er i samsvar med reglene for elementær algebra:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Den første likheten lyder som følger: hvis både A og B er sanne, er produktet A * B sant. I Buhl algebra erstatter multiplikasjonstegnet (*) unionen I.

Logiske produkter kan ikke inneholde to, men et større antall påstander - faktorer. Og i dette tilfellet er produktet sant bare når alle påstander-faktorer er sanne samtidig.

Logisk tillegg (ELLER drift)

Hvis to uttalelser er forbundet av en fagforening OR. den dannede sammensatte setningen kalles en logisk sum.

Tenk på et eksempel på en logisk sum. Å si A: "I dag skal jeg gå på kino."

Uttalelse B: "I dag skal jeg dra til diskoteket." Vi legger til begge utsagnene og får: "I dag skal jeg gå på kino ELLER til et diskotek."

Denne komplekse uttalelsen er betegnet som følger: A + B = C eller (A VB) = C.

Ved C betegnet vi en sammensatt uttalelse av en logisk sum.

I eksemplet som er vurdert kan ikke foreningen OR brukes i eksklusiv forstand. Samme dag kan du faktisk komme på kino og på diskoteket. Og her er ordtaket:

"Styreleder for hagearbeidssamarbeidet vil være Petrov eller Ivanov," er ikke en logisk sum, fordi bare én person vil være formann, og den andre vil være en amatør vanlig gartner.

Tegnet V for den logiske summen er valgt fordi det er den første bokstaven til det latinske ordet "vel", som betyr "eller", i motsetning til det latinske ordet "aut>, som betyr" og ". Nå skal det være klart for alle hvorfor det logiske produktet er indikert med tegnet ^.

I elementær algebra er det en regel A + A = 2A. Denne regelen er sann, uansett hvilket tall som er representert med bokstaven A. I boolsk algebra tilsvarer regelen A + A = A den. Hele livserfaringen vår sier at å si A ELLER A eller begge A bare er en annen og lengre måte å si bare A.

Som ethvert sammensatt utsagn, kan summen av de to utsagnene A og B være sant eller usant. Summen anses som sann, det vil si lik enhet, hvis minst ett av begrepene er sant:

A + B = 1 hvis OR A = 1 ELLER B = 1, noe som stemmer overens med konvensjonell aritmetikk:

1+0 = 0+1 = 1.

Hvis begge oppsummerte utsagn er sanne, blir summen også ansett som sann, derfor har vi i den boolske algebra: (1) + (1) = 1.

Beslagene er satt her for å understreke den betingede, betydningen av dette tillegget og ikke aritmetisk.

Summen av to utsagn anses som usann og lik null hvis, men bare hvis begge begrepene er usanne. Herfra:

0 + 0=0.

Så summen av de to utsagnene A + B regnes som sann hvis sant, ELLER A, ELLER B, ELLER begge betegner sammen. Dermed blir ordet OR betegnet med +.

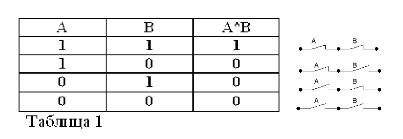
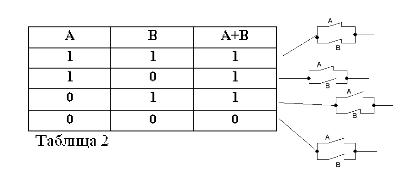
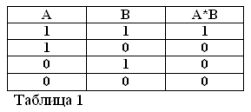
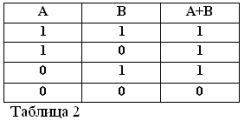
Husk at påstandene A og B bare kan være sanne eller usanne og derfor har et mål på sannhet 1 eller 0, kan resultatene av de vurderte OG- eller ELLER-operasjonene oppsummeres i tabell 1 og 2.

Den tredje operasjonen, mye brukt av Buhl algebra, er negasjonsoperasjonen - IKKE. Vi minner om at elementær algebra bruker operasjonene ADD, D Subtract, Multiply by, Divide by og noen andre.

For hver påstand A er det dens negasjon IKKE A, som vi vil betegne med symbolet / A. Dette skal ikke være i tvil.

Vi gir eksempler: “Vi vil gå til skogen” A, “Vi vil ikke gå i skogen” / A.

Hvis utsagnet A er sant, det vil si A = 1, må dets negasjon / A være usant / A = 0. Og omvendt, hvis noe utsagn er usant, er negasjonen det sant. For eksempel: “En hest spiser ikke hø” / A = 0, “En hest spiser ikke hø” (A = 1). Dette kan komme til uttrykk i tabell 3.

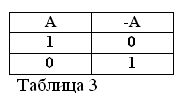
Å bestemme betydningen av handlingen om negasjon, og anta at av de to utsagnene A og / A alltid er en sann, følger to nye formler av den boolske algebra:

A + (/ A) = 1 og A * (/ A) = 0.

Det er også andre formler som forenkler den logiske behandlingen av utsagn. For eksempel 1 + A = 1, ettersom summen, i henhold til definisjonen av tillegg, i tilfelle når ett begrep er lik enhet, summen alltid er lik enhet. Resultatet avhenger ikke av om A = 0 eller A = 1.

Hver av de tre logiske operasjonene vi undersøkte (OG, ELLER, IKKE) har visse egenskaper som ligger nær reglene for elementær algebra. Hvis alle er formulert, så får vi 25 regler for boolsk algebra. De er ganske nok til å løse nesten alle logiske problemer. Uten disse reglene blir det ganske vanskelig å løse logiske problemer på grunn av deres tilsynelatende kompleksitet. Å prøve å finne riktig svar uten å bruke reglene betyr å erstatte dem med oppfinnsomhet og generelle resonnementer. Regler letter dette arbeidet i stor grad og sparer tid.

Innenfor rammen av artikkelen er det umulig å vurdere alle disse 25 reglene, men de som ønsker kan alltid finne dem i relevant litteratur.

Som allerede nevnt i den første artikkelen i 1938, bruker den unge amerikanske forskeren Claude Shannon i sin artikkel "Symbolisk analyse av relé og svitsjekretser" for første gang Boolsk algebra for problemer med reléteknologi. Shannons oppdagelse var at han innså at metoden for å designe stafettmaskiner og elektroniske datamaskiner faktisk er en gren av matematisk logikk.

Det skjer ofte. I mange år har forskeren jobbet med et problem som virker fullstendig unødvendig for landsmennene hans - bare moro. Men flere tiår og noen ganger århundrer går, og en teori som ingen trenger, skaffer seg ikke bare retten til å eksistere, men uten at den videre fremgang blir utenkelig.

Hva hjalp Shannon andre gang med å "oppdage" boolsk algebra? Saken? Ingenting av den typen.

Kjærligheten til stafettmaskiner, bygd på konvensjonelle brytere og stafetter, hjalp den unge forskeren til å koble en glemt teori med oppgavene til automatiske telefonsentraler, som han arbeidet på den tiden. Deretter introduserte Shannon den samme ideen om “ja eller nei” i diskrete meldinger og la grunnlaget for en hel del av kybernetikk - informasjonsteori.

Buhls algebra var veldig egnet for analyse og syntese av stafettkretsløp. Det var nok til å akseptere som et sant utsagn: “Det er et signal i kretsen”, og som en falsk - “Det er ikke noe signal i kretsen”, slik en ny algebra dukket opp - signalalgebra, relékretsalgebra.

Den nye algebraen gjelder bare for vurdering av relé- og koblingskretser. Tross alt er bare i slike ordninger betingelsen "det er et signal" og "ikke noe signal" oppfylt. Der signalet endres kontinuerlig og skaffer et vilkårlig stort antall mellomliggende forhold (et slikt signal kalles analog), er ikke reléalgebra aktuelt. Dette må alltid huskes. Men bare flertallet av elektroniske datamaskiner og kybernetiske maskiner bruker det diskrete prinsippet for signalbehandling, som er basert på elementene “ja - nei”.

Uttrykket "Kontakt stengt" ble akseptert av Shannon som sant (1), og "Kontakt åpen" som usant (0). Resten av "algebraen", inkludert operasjonene AND, OR og NOT og 25 regler, lånte Shannon fra Boole.

Relékretsalgebra viste seg å være enklere enn den boolske algebra, siden den kun omhandler elementer av typen "ja - nei". I tillegg er den nye algebraen mer visuell.

Elementene i denne algebraen er kontaktene, som vi vil betegne med bokstavene A, B, C ... Kontakten er lukket - A, kontakten er åpen - / A (bokstav med strek).

Notasjonen er, som du ser, helt hentet fra boolsk algebra. En åpen kontakt er en negasjon av en lukket kontakt. Den samme kontakten kan ikke være både lukket og åpen.

La oss være enige om at hvis to kontakter er betegnet med samme bokstav, betyr dette at de alltid har de samme verdiene.

Når som helst er de begge åpne på samme tid, eller begge er lukket. Den enkleste måten å forestille seg at de er mekanisk koblet sammen slik at begge åpnes eller lukkes samtidig.

Hvis en kontakt i noen kjede er en negasjon av en annen kontakt, er betydningen deres alltid motsatt. For eksempel kan kontaktene C og / C aldri være åpne eller samtidig lukket. Og i diagrammet kan de bli representert mekanisk koblet: hvis en av dem åpnes, lukkes den andre.

Vi begynner å bli kjent med stafettalgebra ved å analysere de enkleste kretsløpene som tilsvarer AND-, ELLER- og IKKE-operasjonene.

Produktet fra to kontakter (drift OG) er kretsen oppnådd som et resultat av seriekoblingen: den er lukket (lik 1) bare når begge kontaktene er lukket (lik 1).

Summen av to kontakter (ELLER drift) vil være kretsen som dannes når de er koblet parallelt: den er lukket (lik 1) når minst en av kontaktene som danner kretsen er lukket (lik 1).

Det motsatte av denne kontakten (operasjon IKKE) er en kontakt lik 0 (åpen) hvis denne kontakten er 1 (lukket), og omvendt.

Som i den boolske algebra, hvis kontaktene er betegnet med bokstavene A og B, vil vi betegne produktet av to kontakter med A * B, summen med A + B, og kontakten overfor A, av / A. Ovennevnte er forklart i figur 1, 2 og 3.

Gyldighet av tabeller som tilsvarer AND, OR, og IKKE operasjoner. nå skal ingen være i tvil.

La oss dvele ved to eksempler: 1 * 0 = 0 og 1 + 0 = 1.

Det fremgår av figuren at en permanent lukket kontakt koblet i serie med en kontinuerlig åpen kontakt tilsvarer en permanent åpen kontakt (1 * 0 = 0) En permanent lukket kontakt koblet parallelt med en kontinuerlig åpen kontakt tilsvarer en permanent lukket kontakt.

Etter å ha blitt kjent med aritmetikken til kontaktkretser, kan du beskrive enhver relékrets med en formel ved å bruke de aksepterte konvensjonene. I kybernetikk kalles slike formler strukturelle.

Hvis strukturformelen til en relékrets er 1, kan et signal passere gjennom den - kretsen er lukket. Og omvendt, hvis strukturformelen til kretsen er 0, vil signalet ikke passere gjennom det - kretsen er ødelagt.Konklusjon: to stafettkretsløp tilsvarer hverandre når deres strukturelle formler er like.

I fortsettelsen av artikkelen vil vi vurdere eksempler på kontaktkretsløp, typiske kontaktkretsløp og deres ekvivalenter, samt tegne diagrammer i henhold til strukturelle formler. Vi vurderer også de viktigste logiske kretsløpene som utfører funksjonene til boolsk algebra.

Fortsettelse av artikkelen: Boolsk algebra. Del 3. Kontaktordninger

Boris Aladyshkin

Comments

[#1 Alex]

Takk

Bare ett punkt, avsnitt:

"Som i den boolske algebra, hvis kontaktene er betegnet med bokstavene A og B, vil vi betegne produktet av to kontakter med A * B, summen med A + B, og kontakten overfor A, av / A. Ovennevnte er forklart i figur 1, 2 og 3 ..."

Hvor er figur 3?