kategorier: Utvalgte artikler » Begynnerelektrikere
Antall visninger: 57937
Kommentarer til artikkelen: 4
Boolsk algebra. Del 3. Kontaktordninger
 Artikkelen beskriver de grunnleggende prinsippene for utforming av stafettkretsløp i samsvar med en gitt algoritme for deres drift.
Artikkelen beskriver de grunnleggende prinsippene for utforming av stafettkretsløp i samsvar med en gitt algoritme for deres drift.
I to tidligere artikler ble fortalt om det grunnleggende Boolsk algebra og stafett algebra. På dette grunnlaget ble strukturelle formler utviklet, og allerede typiske kontaktkretser ble utviklet på dem.
Det er en enkel sak å tegne en strukturell formel i henhold til et ferdig opplegg. Det er mye vanskeligere å presentere den elektriske kretsen til den fremtidige maskinen i henhold til den ferdige konstruksjonsformelen. Den trenger litt trening!
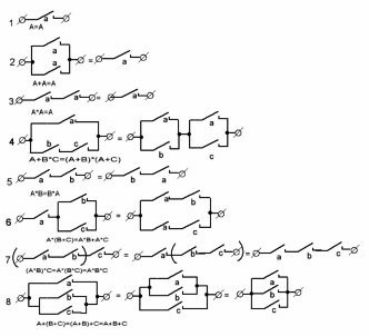
Figur 1 viser de vanligste alternativene. kontaktkretser og deres ekvivalenter. De vil hjelpe til med utarbeidelse av elektriske kretsløp til maskiner, samt analysere ferdige strukturer, for eksempel under reparasjonsprosessen.
Hvordan kan du bruke alternativene for kontaktkretser diskutert ovenfor?
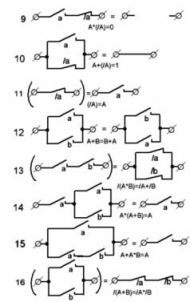
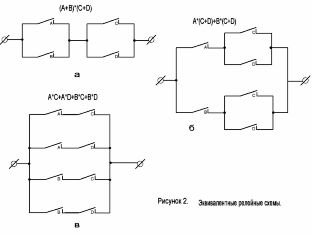
Tenk på kretsen vist i figur 2, a. Den tilsvarende strukturformelen har formen: (A + B) * (C + D).
Ved hjelp av distribusjonsloven for boolsk algebra åpner vi parentesene i dette uttrykket og får: A * (C + D) + B * (C + D), som tilsvarer skjemaet vist i figur 2, b. På grunn av multiplikasjon kan vi videre oppnå formelen A * C + A * D + B * C + B * D, tilsvarende figur 2, c.
Alle tre ordningene er likeverdige, det vil si at de viser seg å være stengt under de samme forhold. Imidlertid er de forskjellige i kompleksitet.
Figur 1. Typiske kontaktkretser
Den første av kretsene, den enkleste, den krever fire reléer, som hver må ha en normalt åpen kontakt. (For å forenkle tegningene vises ikke reléspoler).
Ordningen "b" krever et stafett med to kontaktgrupper. Egentlig er hovedoppgaven til algebra for kontaktkretsløp å finne alle likeverdige kretsløp, slik at du kan velge den enkleste fra dem.
Figur 2. Ekvivalente kontaktkretser.
For å konsolidere materialet som dekkes, prøv å løse følgende problemer selv.
1. Tegn kretsdiagrammet for en automat med strukturformelen A * B * C * D + A * B * E + A * D.
2. Bevis at kretsene som er vist på figur 3, a og b, er likeverdige.
3. Forenkle kretsen vist i figur 3, c.
4. Hvilken strukturformel implementerer ordningen i figur 3, d?
Etter det vi allerede har studert, vil det være mulig å begynne å løse oppgavene som ble satt helt i begynnelsen av den første artikkelen. Vi husker dem kort.
Den første oppgaven var å skru av og på lyspæren i rommet med tre brytere plassert på forskjellige steder: ved døren, ved bordet, ved sengen.
Den andre oppgaven er å stemme sportsdommere: av fire dommere må “FOR” stemme minst to, forutsatt at ”FOR” kommisjonens leder stemte.
Den tredje oppgaven var bare for pedagogiske formål. Det foreslo det samme som i den første, bare for seks brytere, som om det var seks vegger i rommet. Lignende kretser utvikles nettopp ved å bruke algebraen til relékretser.
Generelt, hvis vi ønsker å utvikle et skjema som har noen gitt logiske egenskaper, kan vi tilnærme oss dette problemet på to forskjellige måter. Konvensjonelt kan disse banene kalles "intuitivt" og "algebraisk".
Noen oppgaver løses bedre på den første måten, mens andre på den andre. Den intuitive tilnærmingen viser seg å være mer praktisk når driften av kretsen styres av mange brytere, men det er en viss symmetri i det gjensidige arrangementet av disse reléene. Vi vil se at her en intuitiv tilnærming fører til målet raskere, mens det å bruke apparatet for reléalgebra i tilfelle av mange variabler kan være veldig tungvint. Det er nyttig å bli kjent med begge mulige tilnærminger for å løse dette problemet.
La oss starte med en intuitiv tilnærming. Anta at vi trengte å bygge en krets som var lukket når alle n-styrerelékretser fungerte.
Løsningen på dette problemet krever ikke lang overveielse: det er tydelig at den innstilte betingelsen vil være oppfylt hvis sammenkoblet sekvensielt n normalt åpner relékontakter.
Tilsvarende er det åpenbart at for å bygge en krets som lukkes når minst ett av n-reléene har utløst, er det nok å koble n normalt åpne relekontakter parallelt.
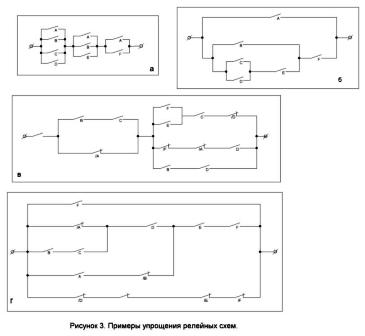
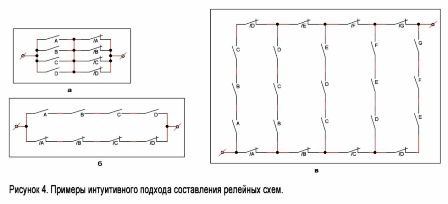
Det er lett å forestille seg en krets som lukkes når noen, men ikke alle, reléer utløses. En slik krets er vist i figur 4, a. Til høyre er et diagram som fungerer etter prinsippet om "alt eller ingenting." Det vil kun være stengt når alle reléer kjøres eller reléene er koblet fra (figur 4, 6).
Tenk nå som et mer sammensatt eksempel. La det være n kontakter som er lokalisert i en bestemt spesifikk sekvens: A, B, C, D, E, F ... Vi vil konstruere en krets som lukkes når noen k-seriekontakter er lukket, og bare de er. Et slikt skjema for verdiene n = 7 og k = 3 er vist i figur 4, c. Metoden for å konstruere slike ordninger for andre verdier av n og k er tydelig fra dette tallet.
Vi fortsetter med å konstruere kretsløp i henhold til de gitte betingelser for deres arbeid ved å bruke reléalgebra.
Som før blir driftsforholdene til kretsen alltid alltid satt muntlig. Designeren må først og fremst kunne sette ord på hva han vil. Hvis han ikke har slik klarhet, vil ingen algebra hjelpe. Du bør alltid starte med en tydelig redegjørelse for kravene som er satt før den nye ordningen. Som i enhver virksomhet, er denne oppgaven kanskje den vanskeligste. Hvis forholdene er enkle nok, kan vi umiddelbart skrive et uttrykk for en strukturell formel som tilfredsstiller disse kravene.
Eksempel 1 Anta at vi må bygge en krets som inneholder 4 kontakter A, B, C og D slik at kretsen slås på når kontakt A er stengt, og en av de tre andre kontaktene. I dette enkle tilfellet vil driften av kretsløpet i muntlig skriving se slik ut: “Kretsen må lede strøm hvis kontaktene A og B er lukket, eller kontaktene A og C eller kontaktene A og D. Enig i at det er veldig enkelt å lage en strukturformel nå. Det vil se slik ut:
A * B + A * C + A * D = 1 eller A * (B + C + D) = 1.
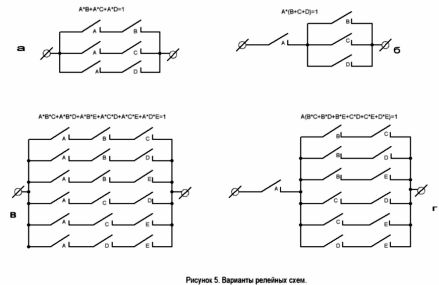
Kretsen har to alternativer. De er vist i figur 5. Det andre alternativet krever ikke et relé med tre normalt åpne kontakter.
Eksempel 2 Den første artikkelen var oppgave nummer 2 om valg av sportsdommere. Les tilstanden nærmere, den ligner på eksemplet nettopp undersøkt. En tydeligere muntlig oversikt over kravene vil se slik ut: “Det er nødvendig å lage en krets som inneholder 5 kontakter A, B, C, D, E, slik at den leder strøm og slår på displaylampen hvis følgende kontakter er lukket:
A og B og C, eller A og B og D, eller A og B og E, eller A og C og D, eller A og C og E, eller A og D og E. Kontakt A er ordførerknappen. Hvis det ikke blir presset, vil hvert av de 6 logiske produktene være 0, dvs. Avstemmingen fant ikke sted.
Strukturformelen vil være som følger:
(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,
eller A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.
Begge varianter av kretsen er vist i figur 5, c og d. Dette er løsningen på problemet.
Når du har litt ferdigheter i å lese strukturformler, er det lett å forestille seg kretsen for selve automaten og alle dens evner. Interessant nok gir algebraen til stafettkretser mer informasjon enn selv kretsen. Den lar deg se hvor mange og hvilke reléer som er nødvendige. Med sin hjelp kan du enkelt finne den enkleste versjonen av kretsmaskinen.
Eksempel 3 Etter å ha fått litt erfaring med utarbeidelse av strukturelle formler, vil vi prøve å løse problemet som startet første artikkel: du må designe en bryter som lar deg slå på lyset når du kommer inn i inngangen og slå av det etter at du har klatret til ønsket gulv, eller omvendt, slå på det når du forlater leiligheten og slå den av etter at du har gått ned. Den samme situasjonen skjer i en lang korridor: i den ene enden må pæren være tent, og etter å ha gått til den andre enden, slukket. Kort sagt, oppgaven koker ned til å kontrollere en lyspære fra forskjellige steder med to brytere.
Vi velger følgende prosedyre for å løse problemet: først formulerer vi tydelig driftsforholdene til bryterne, så skriver vi dem i form av en formel, og vi tegner en elektrisk krets basert på dem.
Så at pæren brant (1), er det nødvendig at en av to betingelser ble oppfylt:
1. Slå på bryteren i bunnen (A) og slå av øverst (/ B). Gå inn på verandaen.
2. Slå på bryteren øverst (B) og skru av bunnen (/ A). Forlater leiligheten.
Ved å bruke den aksepterte notasjonen skrives strukturformelen som følger:
A * (/ B) + (/ A) * B = 1
Kretsdiagrammet til bryteren er vist i figur 6. For øyeblikket er slike brytere kommersielt tilgjengelige, dette er de såkalte gjennombrudd brytere. Derfor blir hensynet til disse ordningene her gitt ganske enkelt for konseptet med de generelle prinsippene for deres arbeid.
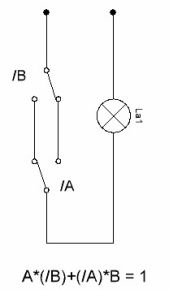
Figur 6
I oppgave nr. 1 i begynnelsen av den første artikkelen, snakket vi om et opplegg som lar deg slå av og på lyset i rommet med en av de tre bryterne. Når vi resonnerer på samme måte som for to brytere, får vi strukturformelen:
A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.
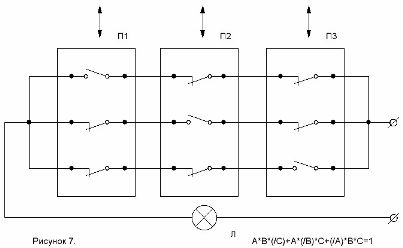
Opplegget utarbeidet med denne formelen er vist i figur 7.
Figur 7
I begynnelsen av den første artikkelen ble en enkel pedagogisk oppgave nr. 2 foreslått: som om det var seks vegger i rommet, og hver av dem hadde en bryter. Logikken i kretsen er nøyaktig den samme som for de tre bryterne. La oss betegne dem med bokstavene A, B, C, D, E, F. Husk at notasjonen (/ A), (/ B) og så videre, dette er ikke et delingstegn, men en logisk negasjon. Oftere indikert ved å understreke karakterer, og til og med hele uttrykk, på toppen. I noen ordninger er denne understrekingen ganske enkelt erstattet av et minustegn. Så strukturformelen for de seks bryterne er:
(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *
(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.
Leserne blir invitert til å lage en komplett elektrisk krets som implementerer denne strukturformelen for å tilegne seg praktiske ferdigheter i å utforme kretsløp. Et lite hint: for kretsen trenger du seks reléer, som hver har en normalt åpen kontakt og fem normalt lukket. Slike komplekse reléer kan om nødvendig settes sammen fra flere enklere ved å koble spolene parallelt.
Dette avslutter historien om boolsk algebra og algebraen til stafettkretser.
Fortsettelse av artikkelen: Logikkbrikker
Boris Aladyshkin
Se også på elektrohomepro.com
: