kategorier: Utvalgte artikler » Begynnerelektrikere
Antall visninger: 48027
Kommentarer til artikkelen: 1
AC kondensatorer
Hva er vekselstrøm?
Hvis vi vurderer en likestrøm, kan den ikke alltid være perfekt konstant: spenningen ved kildeutgangen kan avhenge av belastningen eller av utladningsgraden til batteriet eller det galvaniske batteriet. Selv med konstant stabilisert spenning, er strømmen i den eksterne kretsen avhengig av belastningen, noe som bekrefter Ohms lov. Det viser seg at dette heller ikke er helt konstant strøm, men en slik strøm kan heller ikke kalles variabel, siden den ikke endrer retning.
En variabel kalles vanligvis en spenning eller strøm, hvis retning og styrke ikke endres under påvirkning av eksterne faktorer, for eksempel en belastning, men er helt "uavhengig": det er slik generatoren genererer den. I tillegg bør disse endringene være periodiske, dvs. gjentar over en viss periode kalt en periode.
Hvis spenningen eller strømmen endrer seg, uten å bekymre deg for frekvensen og andre regelmessigheter, kalles et slikt støy. Et klassisk eksempel er "snø" på en TV-skjerm med et svakt sendesignal. Eksempler på noen periodiske elektriske signaler er vist i figur 1.
For likestrøm er det bare to egenskaper: kildens polaritet og spenning. Når det gjelder vekselstrøm, er disse to mengdene tydeligvis ikke nok, så det vises flere parametre til: amplitude, frekvens, periode, fase, øyeblikkelig og effektiv verdi.
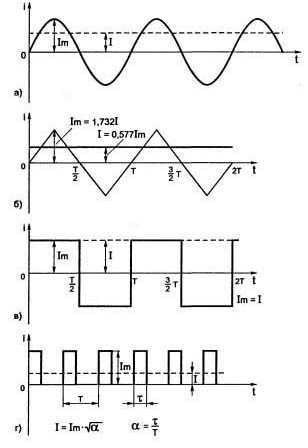
Figur 1Eksempler på noen periodiske elektriske signaler
Oftest innen teknologi har man å gjøre med sinusformede svingninger, dessuten ikke bare innen elektroteknikk. Se for deg et bilhjul. Når du kjører jevn på en god glatt vei, beskriver midten av hjulet en rett linje parallelt med veibanen. Samtidig beveger ethvert punkt på periferien av hjulet seg langs en sinusformet i forhold til den nettopp nevnte linjen.
Det nevnte kan bekreftes av figur 2, som viser en grafisk metode for konstruksjon av en sinusoid: Den som studerte tegning godt vet hvordan man utfører slike konstruksjoner.
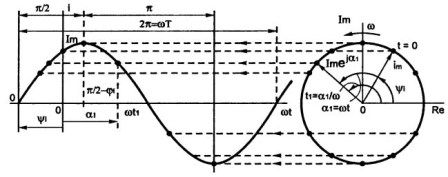
Figur 2Grafisk sinebølgemetode
Fra fysikkens skolekurs er det kjent at en sinus er den vanligste og egnet for å studere en periodisk kurve. På nøyaktig samme måte oppnås sinusformede svingninger i dynamoerpå grunn av deres mekaniske enhet.
Figur 3 viser en graf over sinusstrømmen.
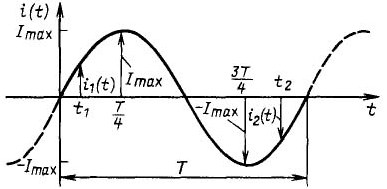
Figur 3Sinusformet gjeldende graf
Det er lett å se at størrelsen på strømmen varierer med tiden, derfor er ordinataksen indikert på figuren som i (t), er funksjonen til strøm versus tid. Hele periode med strømmen er indikert med en solid linje og har en periode T. Hvis du starter betraktningen fra opprinnelsen, kan du se at først strømmen øker, når Imax, går gjennom null, synker til –Imax, deretter øker og når null. Deretter begynner neste periode, som vist med den stiplede linjen.
I form av en matematisk formel skrives den nåværende atferden som følger: i (t) = Imax * sin (ω * t ± φ).
Her i (t) er den øyeblikkelige verdien av strømmen, avhengig av tid, Imax er amplitudeverdien (maksimal avvik fra likevekttilstanden), ω er den sirkulære frekvensen (2 * π * f), φ er fasevinkelen.
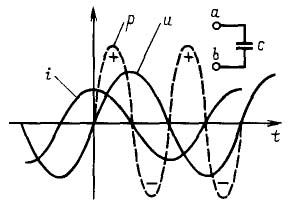
Den sirkulære frekvensen ω måles i radianer per sekund, og fasevinkelen φ i radianer eller grader. Det siste gir mening bare når det er to sinusformede strømmer. For eksempel i kjeder med kondensatoren strømmen ligger foran spenningen 90˚ eller nøyaktig en fjerdedel av perioden, som vist i figur 4. Hvis det er en sinusformet strøm, kan du flytte den langs ordinataksen som du vil, og ingenting vil endre seg fra dette.
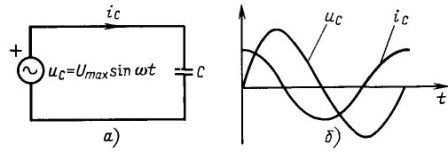
Figur 4 I kretser med kondensator ligger strømmen foran spenningen med et kvarter
Den fysiske betydningen av den sirkulære frekvensen ω er hvilken vinkel i radianer vil "løpe gjennom" en sinusoid på ett sekund.
Periode - T er tiden der sinusbølgen vil gjøre en fullstendig svingning. Det samme gjelder vibrasjoner av en annen form, for eksempel rektangulær eller trekantet. Perioden måles i sekunder eller mindre enheter: millisekunder, mikrosekunder eller nanosekunder.
En annen parameter for et hvilket som helst periodisk signal, inkludert en sinusoid, er frekvensen, hvor mange svingninger signalet vil gjøre på 1 sekund. Måleenheten for frekvens er Hertz (Hz), oppkalt etter forskeren Heinrich Hertz fra 1800-tallet. Så frekvensen på 1 Hz er ikke mer enn en svingning / sekund. For eksempel er lysnettets frekvens 50Hz, det vil si nøyaktig 50 sinusformede perioder på et sekund.
Hvis den nåværende perioden er kjent (du kan måle med et oscilloskop), så vil frekvensen til signalet hjelpe til med å finne ut formelen: f = 1 / T. Hvis tiden er uttrykt i sekunder, vil resultatet dessuten være i Hertz. Motsatt er T = 1 / f, frekvens i Hz, tiden oppnås i sekunder. For eksempel når 50 hertz perioden vil være 1/50 = 0,02 sekunder, eller 20 millisekunder. I strøm brukes oftere høyere frekvenser: KHz - kilohertz, MHz - megahertz (tusenvis og millioner svingninger per sekund), etc.
Alt som er sagt for strøm stemmer også for vekslende spenning: i fig. 6 er det nok å bare endre bokstaven I til U. Formelen vil se slik ut: u (t) = Umax * sin (ω * t ± φ).
Disse forklaringene er nok å komme tilbake til eksperimentere med kondensatorer og forklare deres fysiske betydning.
Kondensatoren leder vekselstrøm, som ble vist i diagrammet i figur 3 (se artikkel - Kondensatorer for AC elektriske installasjoner). Lampens lysstyrke øker når en ekstra kondensator er tilkoblet. Når kondensatorene er koblet parallelt, blir kapasitansene ganske enkelt opp, så det kan antas at kapasitansen Xc avhenger av kapasitansen. I tillegg avhenger det også av frekvensen til strømmen, og derfor ser formelen slik ut: Xc = 1/2 * π * f * C.
Det følger av formelen at med økende kapasitans og frekvens på vekslingsspenningen, reduseres reaktansen Xc. Disse avhengighetene er vist i figur 5.
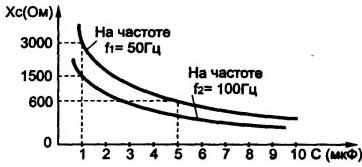
Figur 5. Avhengigheten av reaktansen til kondensatoren på kapasitansen
Hvis vi erstatter frekvensen i Hertz i formelen og kapasitansen i Farads, vil resultatet være i Ohms.
Vil kondensatoren varme opp?
Husk nå opplevelsen med en kondensator og en elektrisk måler, hvorfor snurrer den ikke? Fakta er at måleren vurderer aktiv energi når forbrukeren er en rent aktiv belastning, for eksempel glødelamper, en vannkoker eller en elektrisk komfyr. For slike forbrukere, spenningen og strømmen sammenfaller i fase, har ett tegn: hvis du multipliserer to negative tall (spenning og strøm i løpet av den negative halvsyklusen), er resultatet i henhold til matematikkens lover fortsatt positivt. Derfor er kapasiteten til slike forbrukere alltid positiv, d.v.s. går inn i belastningen og frigjøres i form av varme, som vist i figur 6 med den stiplede linjen.
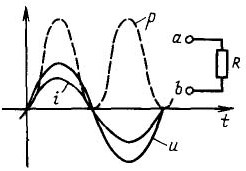
Figur 6
I tilfelle når kondensatoren er inkludert i vekselstrømskretsen, faller ikke strømmen og spenningen i fase: strømmen er 90 оп foran fase i spenning, noe som fører til en kombinasjon når strømmen og spenningen har forskjellige tegn.
Figur 7
I disse øyeblikkene er kraften negativ. Med andre ord, når kraften er positiv, lades kondensatoren, og når den er negativ, overføres den lagrede energien tilbake til kilden. Derfor viser det seg i gjennomsnitt med nuller, og det er rett og slett ingenting å regne her.
Kondensatoren vil ikke en gang varme opp i det hele tatt, med mindre den selvfølgelig kan brukes. Derfor ofte kondensator kalt fri motstand, som tillater bruk i transformatorfrie strømforsyninger med lite strøm.Selv om slike blokker ikke anbefales på grunn av deres fare, er det likevel noen ganger nødvendig å gjøre dette.
Før du installerer i en slik enhet slukkekondensator, bør det sjekkes ved enkel tilkobling til nettverket: hvis kondensatoren ikke har varmet opp på en halv time, kan den trygt inkluderes i kretsen. Ellers må du bare kaste den bort uten å angre.
Hva viser et voltmeter?
Ved fremstilling og reparasjon av forskjellige enheter, selv om det ikke er veldig ofte, er det nødvendig å måle vekslende spenninger og til og med strømmer. Hvis en sinus oppfører seg så hektisk, så opp og ned, hva vil da et normalt voltmeter vise?
Gjennomsnittsverdien av et periodisk signal, i dette tilfellet en sinusoid, beregnes som området avgrenset av abscisseaksen og det grafiske bildet av signalet delt på 2 * π radianer eller sinusoidens periode. Siden de øvre og nedre delene er helt identiske, men har forskjellige tegn, er gjennomsnittsverdien på sinusoidene null, og det er ikke nødvendig å måle den i det hele tatt, og den er til og med meningsløs.
Derfor viser måleapparatet rms-verdien til spenningen eller strømmen. Den gjennomsnittlige kvadratverdien er en slik verdi av den periodiske strømmen hvor den samme mengden varme frigjøres på samme belastning som på likestrøm. Med andre ord lyser pæren med samme lysstyrke.
Dette er beskrevet av formlene som dette: Icr = 0.707 * Imax = Imax / √2 for spenning, formelen er den samme, bare endre en bokstav Ucrc = 0.707 * Umax = Umax / √2. Det er disse verdiene måleapparatet viser. De kan erstattes i formler når du beregner i henhold til Ohms lov eller når du beregner effekt.
Men dette er ikke alt som en kondensator i et AC-nettverk er i stand til. I den neste artikkelen vil vi vurdere bruken av kondensatorer i pulserende kretsløp, høypass- og lavpassfilter, i sinusbølge- og firkantbølgeneratorer.
Boris Aladyshkin
Fortsettelse av artikkelen: Kondensatorer i elektroniske kretsløp
Se også på elektrohomepro.com
: